Volume
6, Number 3, 2019, R1–R57 journal homepage:
region.ersa.org
Volume
6, Number 3, 2019, R1–R57 journal homepage:
region.ersa.orgDOI: 10.18335/region.v6i3.267
REAT: A Regional Economic Analysis Toolbox for R
1 Karlsruhe Institute of Technology, Karlsruhe, Germany Received: 7 June 2019/Accepted: 4 November 2019Abstract. Methods of regional economic analysis are widely used in regional and urban economics as well as in economic geography. This paper introduces the REAT (Regional Economic Analysis Toolbox) package for the programming environment R, which provides a collection of mathematical regional analysis methods in a user-friendly way. The focus is on the identification of regional inequality, beta and sigma convergence, measurement of agglomerations, point-based measures of clustering and accessibility, as well as regional growth. The theoretical basics of the applications are briefly introduced, while the usage of the most important functions is presented and explained using real data.
1 Introduction
Methods of regional economic analysis (or regional analysis) are used frequently in theory-based, empirical studies from regional and urban economics as well as (quantitative) economic geography. These methods aim at analyzing some of the most important issues in the mentioned research fields, including (but not limited to) the existence and evolution of agglomerations, regional economic growth and regional disparities (Capello, Nijkamp, 2009; Dinc, 2015; Farhauer, Kröll, 2014; Schätzl, 2000). In any of the mentioned fields, a growing amount of quantitative data has to be processed when using traditional or novel methods and models of regional analysis. This paper introduces the package (add-on) REAT (Regional Economic Analysis Toolbox) (Wieland, 2019) for the programming environment R (R Core Team, 2018a). The package provides a collection of mathematical regional analysis applications, designed in a relatively user-friendly way.
The main topics in the regional analysis context can be summarized as follows, showing also the structure of the present paper with respect to the presented approaches and their application in REAT:
- Identifying regional inequality (or regional disparities) using indicators of concentration and/or dispersion (Section 2)
- Regional disparities over time leading to the concept of beta and sigma convergence (Section 3)
- Measuring agglomerations, which means the specialization of regions and the spatial concentration of industries as well as more complex cluster indices (Section 4)
- Point-based measures of clustering and accessibility (Section 5)
- Regional growth, especially shift-share analysis (Section 6)
Note that, in its original form, the open source software R is a command-line environment including a lot of mathematical and statistical features. For the installation of R and its packages as well as the basics of navigation and implemented statistical functions, see the R documentations (R Core Team, 2018b). A good supplement for working with R is RStudio (RStudio Team, 2016). The REAT package deals with several R data types: The most functions require and calculate numeric vectors, but, in some cases, also objects of type matrix, data frame and list, depending on the complexity of calculation. For a quick introduction to the data types in R and their properties, see e.g. Kabacoff (2017).
2 Concentration, dispersion and regional disparities
2.1 Indicators of concentration and dispersion
Regional disparities are a frequent topic in economic geography and regional economics. The spatial inequality with respect to e.g. regional output, income or employment is an essential element of polarization theory (Myrdal, 1957) and ”New Economic Geography” (Krugman, 1991; Fujita et al., 2001). Assessing regional disparities is possible using concentration and dispersion indicators, which belong to the univariate and descriptive analysis in statistics. Apart from regional economics, these measures are used in several contexts, such as competition economics (market concentration of firms) or welfare economics (income inequality). For a review of the most common indicators with respect to regional inequality, see Portnov, Felsenstein (2010), for studies comparing different indicators in the regional economic context using empirical data, see e.g. Gluschenko (2018); Habánik et al. (2013); Huang, Leung (2009); Palan (2017); Petrakos, Psycharis (2016).
Concentration is operationalized as the discrepancy between an empirical distribution of a variable x (e.g. annual turnover, income, gross domestic product [GDP]) with n observations or objects (e.g. competing firms, households, regions) and a (theoretical) equal distribution or a reference distribution (e.g. population distribution). Dispersion indicators aim at the deviation from the arithmetic mean of x, . In this context, Portnov, Felsenstein (2005, 2010) distinguish between measures of deprivation and variation.
Typical measures of regional disparities are the Gini coefficient, the Herfindahl-Hirschman index and the coefficient of variation (Lessmann, 2005). The most popular measure of concentration is the Gini coefficient (Gini, 1912) in combination with the Lorenz curve (Lorenz, 1905). There are several calculation approaches for the Gini coefficient, all producing the same result. The Lorenz curve is a graphical indicator, showing the deviation of the empirical shares of the regarded variable x from a (theoretical) equal distribution. Another well-known indicator is the Herfindahl-Hirschman index, which was developed independently by Hirschman (1945) and Herfindahl (1950), both in the context of competition economics. Several other concentration indicators are also applied in the fields of regional economics with respect to regional disparities, such as the Hoover coefficient (Hoover, 1936) and the Theil coefficient (Theil, 1967).
Except for the standard deviation, whose unit is equal to the unit of x, all common indicators are dimensionless. Most of them (except for standard deviation and coefficient of variation) have a fixed value range, normally between zero (indicating complete equality/dispersion) and one (indicating complete inequality/concentration).
Most of the common indicators are mathematically formulated in an unweighted and in a weighted form, while, in the context of regional disparities, the latter is mostly done using the regions’ proportion of the total (e.g. national) population (Doran, Jordan 2013; Lessmann 2014; Mussini 2017; Petrakos, Psycharis 2016; for a critical discussion of weighting these coefficients, see Gluschenko 2018). In the literature, there are different formulations where the weighted coefficients also include a weighted arithmetic mean. Note that, in the case of the population-weighted Gini coefficient, a weighted arithmetic mean is mandatory to keep the indicators’ value range.
Especially when dealing with GDP per capita as an indicator of regional economic output, several recent studies use dispersion measures rather than concentration measures, especially the (weighted) coefficient of variation (e.g. Lessmann 2005, 2014, 2016; Lessmann, Seidel 2017; Petrakos, Psycharis 2016). This dispersion indicator is a dimensionless normalization of the standard deviation. Weighting the coefficient of variation with population shares was introduced by Williamson (1965), which has led to calling this coefficient the Williamson index. As regional incomes or outputs are not normally distributed in most cases, resulting in biased arithmetic means used in the calculation of dispersion measures, the regarded variable may be log-transformed, which means replacing xi with log(xi) in the calculations.
Table 1 shows the common indicators, including their (population-)weighted and their normalized form (if there exist any) and the corresponding value ranges. The formulae are shown in a way that includes several ways of application. The regarded variable is always named xi, while the (population) weighting is called wi. Some indicators, such as the Hoover or the Coulter coefficient, require a variable representing a reference distribution the shares of xi are compared to. This reference is not a weighting. However, in many studies, the regional population is also used for the reference distribution. In these cases, reference and weighting are the same data. The reference distribution may also be equal to 1∕n.
Several indicators are also used for the analysis of regional specialization or the spatial concentration of industries, such as the Hoover coefficient or the Herfindahl-Hirschman index or its inverse (1∕HHI; also known as the “equivalent number” in the competition context). Other coefficients of concentration and specialization are discussed in Section 4. The last coefficient in Table 1, the mean square successive difference (von Neumann et al., 1941) is a measure for time variability not originating from but also transferable to regional economics.
| Indicator | Unweighted | Weighted | Normalized |
| Gini | G = 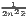 ∑
i=1n∑
j=1n ∑
i=1n∑
j=1n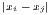 | Gw =  ∑
i=1n∑
j=1nw
iwj ∑
i=1n∑
j=1nw
iwj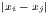 | G* =  G G |
0 ≤ G ≤ 1 -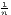 | 0 ≤ G ≤ 1 -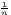 | 0 ≤ G*≤ 1 | |
| HHI | HHI = ∑
i=1n(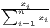 )2 )2 | HHI* = 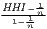 |
|
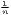 ≤ HHI ≤ 1 ≤ HHI ≤ 1 | 0 ≤ HHI*≤ 1 | ||
| Hoover | HC = | HCw = | |
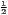 [∑
i=1n| [∑
i=1n|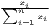 - -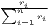 |] |] | 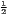 [∑
i=1nw
i| [∑
i=1nw
i|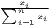 - -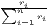 |] |] | ||
| 0 ≤ HC ≤ 1 | 0 ≤ HC ≤ 1 | ||
| Theil | TC = 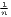 ∑
i=1n ln( ∑
i=1n ln(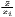 ) ) | TCw = 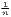 ∑
i=1nw
i ln( ∑
i=1nw
i ln(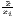 ) ) | |
| 0 ≤ TC ≤ 1 | 0 ≤ TCw ≤ 1 | ||
| Coulter | CC = | ||
![∘ 1-∑n-------xi------ri--2-
2[ i=1wi(∑ni=1xi - ∑ni=1ri)]](26725x.png) | |||
| 0 ≤ CC ≤ 1 | |||
| Atkinson | AI = 1 - [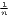 ∑
i=1nx
i1-ϵ] ∑
i=1nx
i1-ϵ]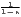
| ||
| 0 ≤ AI ≤ 1 | |||
| Dalton | δ = 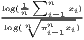 | ||
| 0 ≤ δ ≤∞ | |||
| SD | s = 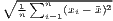 | sw =  | see CV |
| 0 ≤ s ≤∞ | 0 ≤ s ≤∞ | ||
| CV | v = 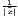 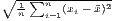 | see Williamson | v* = 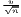 |
| 0 ≤ v ≤∞ | 0 ≤ v*≤ 1 | ||
| Williamson | WI = 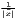  | ||
| 0 ≤ v ≤∞ | |||
| MSSD | MSSD = 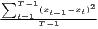 | ||
Notes: xi is the i-th observation of the regarded variable x (e.g. GDP [per capita] in region i), xj is the value of the same variable with respect to object j, ri is the i-th observation of a reference variable (e.g. population), n is the number of objects (e.g. regions), is the arithmetic mean of x: =
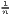 ∑
i=1nx
i, w is the weighted arithmetic mean
of x: w =
∑
i=1nx
i, w is the weighted arithmetic mean
of x: w = 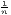 ∑
i=1nw
ixi, wi and wj are the population weightings: Pi∕∑
i=1nP
i and Pj∕∑
j=1nP
j, where Pi
and Pj are the population sizes of regions i and j, respectively, ϵ is an inequality aversion parameter
(0 < ϵ < ∞) for the Atkinson index, t is a given time period and T is the number all regarded time
periods.
∑
i=1nw
ixi, wi and wj are the population weightings: Pi∕∑
i=1nP
i and Pj∕∑
j=1nP
j, where Pi
and Pj are the population sizes of regions i and j, respectively, ϵ is an inequality aversion parameter
(0 < ϵ < ∞) for the Atkinson index, t is a given time period and T is the number all regarded time
periods.
Compiled from: Charles-Coll (2011); Cracau, Durán Lima (2016); Damgaard, Weiner (2000); Gluschenko (2018); Heinemann (2008); Kohn, Öztürk (2013); Portnov, Felsenstein (2005, 2010); Taylor, Cihon (2004); Schätzl (2000); Störmann (2009)
2.2 Application in REAT
2.2.1 REAT functions for concentration and dispersion indicators
Table 2 shows the functions for concentration and dispersion measures implemented in the REAT package. All functions require at least one argument, a numeric vector with a length equal to n, containing the regarded variable x (e.g. income) with i observations (e.g. regions), where i = 1,...,n. This data may be a single vector or a column of a data frame or matrix.
An optional weighting of the vector x can be done using the function argument weighting which is also a numeric vector of length n. By default, the functions remove missing (NA) values. The hoover() function always needs a reference distribution (see the Hoover coefficient formula in Table 1), which is stated via the ref argument, also requiring a numeric vector of length n. If no reference variable is stated (ref = NULL), the reference is set to 1∕n.
All functions (except for disp()) return the single value of the computed coefficient. In the relevant cases (gini(), gini2(), herf() and cv()), a normalization of the coefficient is possible using the function argument coefnorm = TRUE, returning the normalized coefficient instead of the raw coefficient. The function disp() is a wrapper for all mentioned functions, calculating all coefficients (except for the MSSD) at once for one vector x or a set of variables/columns from a data frame or matrix.
Note that there are two functions for the Gini coefficient, gini() and gini2(), both producing the same result in the unweighted case. The former function is designed for income inequality, where the weighting option is designed for the calculation of the Gini coefficient for groups (e.g. income classes), where the weighting represents the group mean. The function gini2() is designed for the population-weighted analysis of regional inequality.
| Indicator | REAT function | Mandatory arguments | Optional arguments | Output |
| Gini/ | gini() | vector x | weighting vector, | value: G or G* |
| Lorenz | remove NAs, | or Gw, | ||
| Lorenz curve, | optional: plot (LC) | |||
| normalization | ||||
| gini2() | vector x | weighting vector Pi, | value: G or G* | |
| remove NAs, | or Gw, | |||
| normalization | ||||
| lorenz() | vector x | weighting vector, | plot LC, | |
| remove NAs, | value: G or Gw | |||
| and/or G* | ||||
| HHI | herf() | vector x | remove NAs, | value: HHI or |
| normalization | HHI* or NHHI | |||
| Hoover | hoover() | vector x | weighting vector Pi, | value: HC or HCw |
| reference vector ri | remove NAs | |||
| Theil | theil() | vector x | weighting vector Pi, | value: TC or TCw |
| remove NAs | ||||
| Coulter | coulter() | vector x | weighting vector Pi, | value: CC |
| remove NAs | ||||
| Atkinson | atkinson() | vector x | remove NAs, | value: AI |
| epsilon | ||||
| Dalton | dalton() | vector x | remove NAs | value: δ |
| SD | sd2() | vector x | weighting vector, | value: s or sW |
| remove NAs, | ||||
| treating as sample | ||||
| CV | cv() | vector x | weighting vector, | value: v or vW |
| remove NAs, | or v* | |||
| normalization, | ||||
| treating as sample | ||||
| Williamson | williamson() | vector x, | remove NAs | value: WI |
| weighting | ||||
| vector Pi | ||||
| MSSD | mssd() | vector x | remove NAs | value: MSSD |
| All indicators | disp() | vector x | weighting vector Pi, | matrix with 13 |
| or vectors x1,x2,... | remove NAs | (no weighting) | ||
| from dataframe | or 19 indicators | |||
| (incl. weighted) | ||||
Source: own compilation.
2.2.2 Application example: Small-scale regional disparities in health care provision
Regional inequality with respect to health care providers is a topic of high societal significance. In Germany, the health care planning system (Kassenärztliche Bedarfsplanung) attempts to flatten the disparities of local health care provision (Kassenärztliche Bundesvereinigung, 2013). Here, we analyze small-scale regional disparities in health care provision in two neighboring German counties (Göttingen and Northeim) using the data on medical practices and local population from Wieland, Dittrich (2016). The data is stored in the datasets GoettingenHealth1 and GoettingenHealth2, both included as example datasets in the REAT package. The study area is segmented into 420 districts, representing either city districts of larger cities or villages and hamlets.
The dataset GoettingenHealth2 contains these 420 regions with an individual ID (column district) and geographic coordinates (columns lat and lon, respectively) and the number of general practitioners, psychotherapists and pharmacies located there (columns phys_gen, psych and pharm, respectively) as well as the local population (column pop). First, we load the dataset:
Now, we investigate how the health care providers are dispersed over the whole area. In the first step, we calculate the Gini coefficient for the concentration of general practitioners using the REAT function gini():
[1] 0.8386269
The empirical Gini coefficient is equal to 0.839, indicating a relatively strong concentration. If we want to calculate the normalized (unbiased) indicator instead, we use the same function with the optional argument coefnorm = TRUE:
[1] 0.8406284
In the same way, we calculate e.g. the Herfindahl-Hirschman index, non-normalized and normalized:
[1] 0.01528053
herf (GoettingenHealth2$phys_gen, coefnorm = TRUE)
[1] 0.01293036
Remember that the minimum of HHI is 1∕n (here: 1∕420 ≈ 0.00238) and the minimum of HHI* is equal to zero.
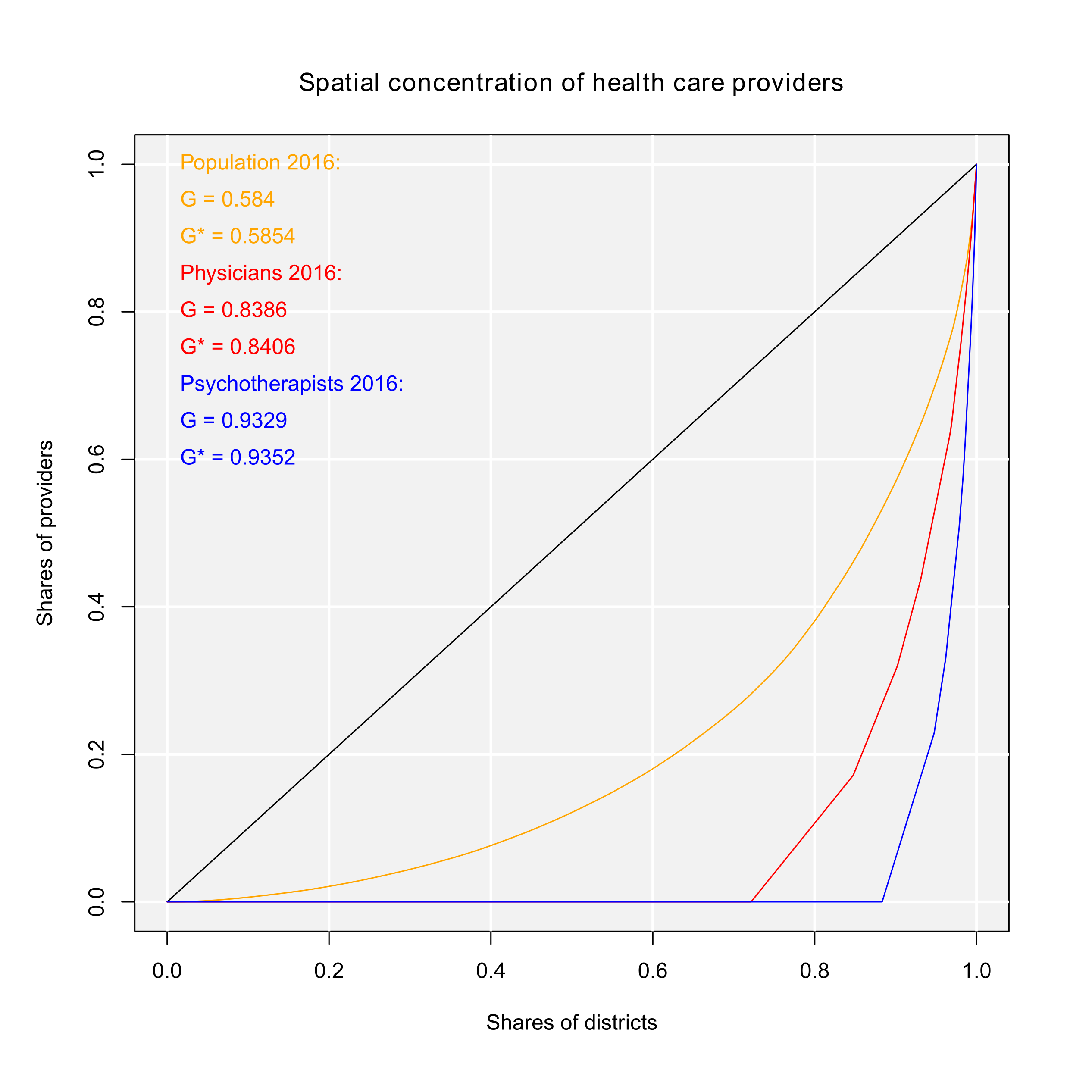
If we want to inspect the concentration graphically, we could use the Lorenz curve, which can be plotted using either the functions gini() or lorenz(). Here, we use gini(), tell the function to plot the curve (lc = TRUE), and include several graphical parameters (such as lc.col for the color of the Lorenz curve or lcx and lcy for the x/y axes labels). As we want to compare the population distribution to the location distribution, we start by plotting the Lorenz curve for the local population:
lc.col = "orange", lcx = "Shares of districts", lcy = "Shares of
providers", lctitle = "Spatial concentration of health care
providers", lcg = TRUE, lcgn = TRUE, lcg.caption =
"Population 2016:", lcg.lab.x = 0, lcg.lab.y = 1)
# Gini coefficient and Lorenz curve for the no. of inhabitants
[1] 0.5840336
Now, we overlay the Lorenz curves of general practitioners and psychotherapists, which means adding two more curves (function argument add.lc = TRUE):
lc.col = "red", lcg = TRUE, lcgn = TRUE, lcg.caption =
"Physicians 2016:", lcg.lab.x = 0, lcg.lab.y = 0.85)
# Adding Gini coefficient and Lorenz curve for the general practitioners
[1] 0.8386269
gini(GoettingenHealth2$psych, lsize = 1, lc = TRUE, add.lc = TRUE,
lc.col = "blue", lcg = TRUE, lcgn = TRUE, lcg.caption =
"Psychotherapists 2016:", lcg.lab.x = 0, lcg.lab.y = 0.7)
# Adding Gini coefficient and Lorenz curve for psychotherapists
[1] 0.9329298
Our commands result in the output of Figure 1, showing three Lorenz curves (population, general practitioners and psychotherapists) and the line of equality (diagonal). All three empirical distributions differ from an equal distribution. In about 72% of the regions, representing about 23% of the whole population (orange curve; G ≈ 0.584), no general practitioner is located (red curve; G ≈ 0.839). But the psychotherapists are more concentrated, as they are located only in about 13% of all districts (blue curve; G ≈ 0.933). As we can see, the physicians are more concentrated than the inhabitants but the psychotherapists are more concentrated than the physicians.
Now, we calculate all mentionened concentration and dispersion coefficients at once for all three types of providers using the function disp(), including a population weighting:
# column 5 = general practitioners, column 6 = psychotherapists,
# column 7 = pharmacies, column "pop" = local population
Our output is:
Note: w = weighted, n = normalized, eq = equivalent number
phys_gen psych pharm
Gini 0.838626907 0.932929782 0.891547619
Gini n 0.840628403 0.935156345 0.893675418
Gini w 0.629454516 0.770895945 0.705628058
Gini w n 0.630956794 0.772735792 0.707312135
HHI 0.015280527 0.038494685 0.024166667
HHI n 0.012930361 0.036199923 0.021837709
HHI eq 65.442769020 25.977611940 41.379310345
Hoover 0.721428571 0.883333333 0.838095238
Hoover w 0.001852337 0.003130602 0.003418787
Theil NA NA NA
Theil w NA NA NA
Coulter 0.049850824 0.123305927 0.065569205
Atkinson 0.761164110 0.900755425 0.854223763
Dalton NA NA NA
SD 1.714506606 1.095496987 0.865286915
SD w 4.010246439 1.847716870 2.401476794
CV 2.330397328 3.899226565 3.028504203
CV n 0.113847359 0.190489683 0.147952112
Williamson 1.429449565 1.965446423 1.709288672
We conclude that any concentration/dispersion measure is the highest for psychotherapists and the lowest for the general practitioners, while the values for pharmacies lie between them. The regional disparities with respect to pharmacies are higher than those with respect to general practitioners, while the most unequal distribution is that of psychotherapists. In other words: The pharmacies are more spatially concentrated than the general practitioners and the psychotherapists are the most concentrated health locations here.
In most cases, population weighting reduces the coefficient values. That is, because districts with a large (small) population have a high (low) impact on the resulting coefficient and the districts without health service providers are also small districts. Furthermore, as the regarded variables contain zero values (which means no health service locations), the Theil coefficient (including the term ln(∕xi)) and the Dalton coefficient (including the n-th root) cannot be computed, resulting in an output of NA.
The visible output of any function presented above can be saved in a new R object:
# save as gini_phys (numeric vector of length = 1)
We can simply access our result:
[1] 0.8386269
The function disp() returns a matrix with 13 rows (when only unweighted coefficients are computed) or 19 rows (in the case of additional weighted coefficients) and one column for each regarded variable:
weighting = GoettingenHealth2$pop)
# save as disp_Goettingen (matrix)
We call our results:
phys_gen psych pharm
Gini 0.83862691 0.93292978 0.89154762
Gini n 0.84062840 0.93515634 0.89367542
...
3 Regional convergence
3.1 The concept of beta and sigma convergence
Regional convergence is derived from (regional) growth theory (for an extensive survey, see Barro, Sala-i Martin 2004) and means the decline of regional disparities over time. The neoclassical growth model states that a region’s economic output (e.g. GDP per capita) depends on its stock of factors of production, capital and labor (aggregate production function), on condition of constant returns to scale and diminishing marginal product of the factor inputs. As a consequence, regions with a high (low) initial level of factor input grow slower (faster) than “poor” (“rich”) regions, what is called beta convergence. It is assumed that all regions converge to the same regional output level (steady-state). Sigma convergence means the decline of regional inequality with respect to regional output over time itself (Allington, McCombie, 2007; Capello, Nijkamp, 2009).
Both types of convergence can be tested empirically, as presented in Table 3. When testing for beta convergence, the natural logarithms of output growth over T time periods in i regions is regressed against the natural logarithms of the initial output values at time t. The original convergence formula was presented by Barro, Sala-i Martin (2004) using a nonlinear least squares (NLS) estimation approach. But in many cases, a linear transformation is used which allows for ordinary least squares (OLS) estimation (Allington, McCombie, 2007; Dapena et al., 2016; Schmidt, 1997; Young et al., 2008). The outcome variable of the convergence equation can be the regional growth between two years (e.g. Young et al. 2008) or the average growth rate per year (e.g. Goecke, Hüther 2016; Puente 2017; Weddige-Haaf, Kool 2017). Significance tests are carried out with t-tests for the regression coefficients and, in the OLS case, the F-test for the significance of R2.
The estimated parameter of interest is the slope of the model, here denoted β (that is why the modeled process is called beta convergence): If β < 0 and statistically significant, there is absolute beta convergence. If additional variables (conditional variables) are included into the convergence equation, we have a test for conditional beta convergence. A further interpretation of the β coefficient is possible using the speed of convergence, λ, and H, the so-called half-life, which means the time (measured in the regarded time periods) to reduce the regional disparities by one half (Allington, McCombie, 2007; Schmidt, 1997).
Sigma convergence (which is named after the Greek letter for the standard deviation, σ) can be tested in two ways depending on the number of time periods: The regional inequality between all regions at time t is measured using the standard deviation, σt, or the coefficient of variation, cvt, for the GDP per capita in its original or natural-logged form. If only two years are regarded, the quotient of both parameters is computed. If e.g. σt1 > σt2, the regional inequality has declined from t1 to t2. A significance test can be applied with a simple ANOVA (analysis of variance), where the test statistic is the quotient of the underlying variances (σ2) (Furceri, 2005; Schmidt, 1997; Young et al., 2008). Within a time series, the dispersion parameter is regressed (and plotted) against time. If the slope coefficient of time is negative, there is sigma convergence (Goecke, Hüther, 2016; Huang, Leung, 2009; Schmidt, 1997).
| Type of convergence | Two time periods | More than two time periods | |
| Beta convergence | absolute
| ||
| and estimation type | NLS | NLS | |
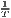 ln( ln(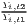 ) = ) = | 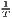 ∑
t=1T ln( ∑
t=1T ln(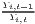 ) = ) = |
||
α - [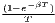 ] ln(Y i,t1) + ϵ ] ln(Y i,t1) + ϵ | α - [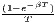 ] ln(Y i,t1) + ϵ ] ln(Y i,t1) + ϵ |
||
| OLS | OLS | ||
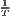 ln( ln(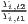 ) = ) = | 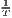 ∑
t=1T ln( ∑
t=1T ln(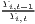 ) = ) = | ||
| α + β ln(Y i,t1) + ϵ | α + β ln(Y i,t1) + ϵ | ||
| conditional | |||
| NLS | NLS | ||
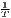 ln( ln(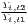 ) = ) = | 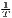 ∑
t=1T ln( ∑
t=1T ln(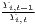 ) = ) = |
||
α - [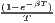 ] ln(Y i,t1) + θXi + ϵ ] ln(Y i,t1) + θXi + ϵ | α - [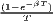 ] ln(Y i,t1) + θXi + ϵ ] ln(Y i,t1) + θXi + ϵ |
||
| OLS | OLS | ||
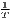 ln( ln(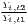 ) = ) = | 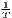 ∑
t=1T ln( ∑
t=1T ln(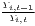 ) = ) = | ||
| α + β ln(Y i,t1) + θXi + ϵ | α + β ln(Y i,t1) + θXi + ϵ | ||
| β < 0 | β < 0 | ||
| Convergence speed: λ =
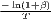 | |||
| Half-life: H =
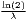 | |||
| Sigma convergence | σt = 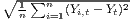 or or | ||
| cvt = 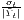 | |||
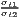 > 1 or > 1 or | σ = a + bt + ϵ or | ||
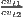 > 1 > 1 | cv = a + bt + ϵ | ||
Test statistic: 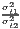 | b < 0 | ||
Notes: Y i,t is the regional output (e.g. GDP per capita) of region i at time t, t is the arithmetic mean of Y i,t for all regions at time t, T is the number of regarded time periods (e.g. years), Xi is a set of other variables (conditions), σt is the standard deviation of the regional output of all regions, cvt is the corresponding coefficient of variation, α, β, θ, a and b are estimated coefficients, ϵ is an error term and n is the number of regions.
Compiled from: Allington, McCombie (2007); Barro, Sala-i Martin (2004); Furceri (2005); Schmidt (1997)
3.2 Application in REAT
3.2.1 REAT functions for beta and sigma convergence
Table 4 shows the functions for beta and sigma convergence as implemented in REAT. The analysis of beta convergence is provided by the functions betaconv.ols() and betaconv.nls() for OLS and NLS estimation, respectively. Speed of convergence and half-life can be computed with the function betaconv.speed(). The ratio test of sigma convergence for two time periods can be done using the function sigmaconv(), while a trend regression over time is implemented into the function sigmaconv.t(). Both convergence types can be analyzed at once with the function rca(), which is a wrapper for all functions mentioned above.
The functions require (at least) two numeric vectors, containing the regarded variable Y (e.g. GDP per capita) for at least two different time periods, e.g. from the same data frame. Also the start and end time periods (t1 and tT) have to be stated. Optionally, a graphical output can be generated (scatterplot for beta convergence, line plot for sigma convergence with respect to longitudinal data). Furthermore, when analyzing sigma convergence, the user can choose whether Y should be log-transformed or not and/or which sigma measure is computed (variance, standard deviation or coefficient of variation; weighted or non-weighted).
Note that, unlike the functions for regional inequality indicators (Section 2), the REAT functions for regional convergence distinguish between a visible and an invisible output. The latter can be saved as a new R object. While the visible output shows the main results, the invisible output goes beyond that: betaconv.ols(), betaconv.nls() and rca() return a list, which is the most flexible data type in R, because it consists of a non-predetermined number of different data objects. Apart from the model results, e.g. the (transformed) regression data is returned in this invisible output.
| Convergence | REAT function | Mandatory arguments | Optional arguments | Output |
| Beta | betaconv.ols() | vectors Y i,t1 and | Conditions, | visible: model |
| convergence | Y i,t2,...,Y i,T, | scatterplot | estimates, invisible: | |
| t1 and tT | list with model | |||
| estimates and | ||||
| regression data, | ||||
| optional: plot | ||||
| betaconv.nls() | vectors Y i,t1 and | Conditions, | visible: model | |
| Y i,t2,...,Y i,T, | scatterplot | estimates, invisible: | ||
| t1 and tT | list with model | |||
| estimates and | ||||
| regression data, | ||||
| optional: plot | ||||
| betaconv.speed() | values β | matrix with | ||
| and T | λ and H | |||
| Sigma | sigmaconv() | vectors Y i,t1 and | Sigma measure, | visible: estimates, |
| convergence | (when T = 2) | Y i,t2, t1 and tT | log, weighting, | invisible: matrix |
| normalization | with estimates | |||
| sigmaconv.t() | vectors Y i,t1 and | Sigma measure, | visible: model | |
| (when T > 2) | Y i,t2,...,Y i,T, | log, weighting, | estimates, invisible: | |
| t1 and tT | normalization, | matrix with | ||
| line plot | model estimates, | |||
| optional: plot | ||||
| All at once: | ||||
| Beta and | rca() | vectors Y i,t1 and | Beta estimation, | visible: model |
| sigma | Y i,t2,...,Y i,T, | conditions, | estimates, invisible: | |
| convergence | t1 and tT | scatterplot, | list with model | |
| sigma measure, | estimates and | |||
| log, weighting, | regression data, | |||
| line plot | optional: plot | |||
Source: own compilation.
3.2.2 Application example: Beta and sigma convergence in Germany on the county level
In this example, we look at regional convergence in Germany. The REAT package includes the example dataset G.counties.gdp with the GDP (gross domestic product), the population and the GDP per capita for the 402 counties (“Kreise”) in Germany 1992 to 2014 (complete data only for 2000-2014). First, we load the dataset:
In our case, we prevent scientific notation of numbers in R and set a limit of 4 digits:
We need the columns named gdppcxxxx, containing the GDP per capita for each year, e.g. G.counties.gdp$gdppc2010 contains the GDP per capita for 2010. In the first step, we test absolute beta convergence comparing the years 2010 and 2014 with OLS estimation using the function betaconv.ols():.
2014, output.results = TRUE)
# Two years, no conditions (Absolute beta convergence)
The output is:
Model coefficients (Estimation method: OLS)
Estimate Std. Error t value Pr (>|t|)
Alpha 0.104159 0.018934 5.501 0.00000006743
Beta -0.007373 0.001848 -3.990 0.00007867475
Lambda 0.001850 NA NA NA
Halflife 374.640507 NA NA NA
Model summary
Estimate F value df 1 df 2 Pr (>F)
R-Squared 0.03827 15.92 1 400 0.00007867
We see that both regression coefficients, α and β, are statistically significant (t ≈ 5.50 and -3.99, respectively, both p < 0.001) and the linear regression model is significant as a whole (F ≈ 15.92, p < 0.001). The negative sign of β shows that, on average, the higher the initial GDP per capita, the lower its growth, which indicates absolute beta convergence. However, the convergence process is very slow: The speed of convergence, represented by λ, shows a harmonization by 0.185% per year. This implies that the output gap will be reduced by 50% in approximately 375 years.
Now we check sigma convergence for the same time using the function sigmaconv(). We choose the coefficient of variation as measure, while using the GDP per capita values in their original form:
2014, sigma.measure = "cv", output.results = TRUE)
# Using the coefficient of variation
The output is:
Estimate F value df1 df2 Pr (>F)
CV 2010 0.03416 NA NA NA NA
CV 2014 0.03316 NA NA NA NA
Quotient 1.03004 1.038 401 401 0.7117
The coefficient of variation is a little smaller in 2014, which means the spatial inequality declined between 2010 and 2014. The quotient of the variances is slightly above one (F = σ20102∕σ20142 ≈ 1.04), but not statistically significant (p ≈ 0.71).
When analyzing regional convergence with REAT, it is preferable (and more convenient) to use the wrapper function rca(). Instead of repeating the results above, we test for (absolute) beta and sigma convergence between 2000 and 2014. The analysis of sigma convergence uses trend regression (function argument sigma.type = "trend") for the coefficient of variation (sigma.measure = "cv"). We also want plots for both convergence types (beta.plot = TRUE and sigma.plot = TRUE, respectively) with specific axis labels (e.g. beta.plotX = "Ln (initial GDP p.c.)"). Our code is:
conditions = NULL, sigma.type = "trend", sigma.measure = "cv",
beta.plot = TRUE, beta.plotLine = TRUE, beta.plotX =
"Ln (initial GDP p.c.)", beta.plotY = "Ln (av. growth GDP p.c.)",
beta.plotTitle = "Beta convergence of German counties 2000-2014",
sigma.plot = TRUE, sigma.plotY = "cv of ln (GDP p.c.)",
sigma.plotTitle = "Sigma convergence of German counties 2000-2014")
# 14 years: 2000 (column 55) to 2014 (column 68)
# no conditions (Absolute beta convergence)
# with plots for both beta and sigma convergence
This results in the following output:
Absolute Beta Convergence
Model coefficients (Estimation method: OLS)
Estimate Std. Error t value Pr (>|t|)
Alpha 0.0954564 0.0099087 9.634 0.00000000000000000006845
Beta -0.0071323 0.0009885 -7.215 0.00000000000271925822550
Lambda 0.0005113 NA NA NA
Halflife 1355.7282963 NA NA NA
Model summary
Estimate F value df 1 df 2 Pr (>F)
R-Squared 0.1152 52.06 1 400 0.000000000002719
Sigma convergence (Trend regression)
Estimate Std. Error t value Pr(>|t|)
Intercept 0.5523659 0.03084855 17.91 0.0000000001526
Time -0.0002579 0.00001537 -16.78 0.0000000003446
Model summary
Estimate F value df 1 df 2 Pr (>F)
R-Squared 0.9558 281.4 1 13 0.0000000003446
This function also produces the plots in Figures 2a and 2b, both showing a declining curve, which is a first indication of both beta and sigma convergence. The beta convergence model is statistically significant (F ≈ 52.06, p < 0.001), as well as the coefficients α (t ≈ 9.63, p < 0.001) and β (t ≈-7.21, p < 0.001). Again, we find evidence for absolute beta convergence because of a negative slope (β ≈-0.007). The trend regression model for sigma convergence is significant (F ≈ 281.4, p < 0.001). The slope is significant and negative (b ≈-0.00026, t ≈ 17.91, p < 0.001), which indicates sigma convergence. However, both types of convergence can be regarded as very slow processes: The half-life value shows that, resulting from the beta convergence model, the regional disparities in GDP per capita will be halved in approximately 1,356 years. When looking at the trend regression, we see that the coefficient of variation declines only by 0.00026 per year. Another aspect is that we only regarded absolute beta convergence, ignoring other spatial effects or the impact of regional policy. The latter is also not considered in neoclassical regional growth theory.
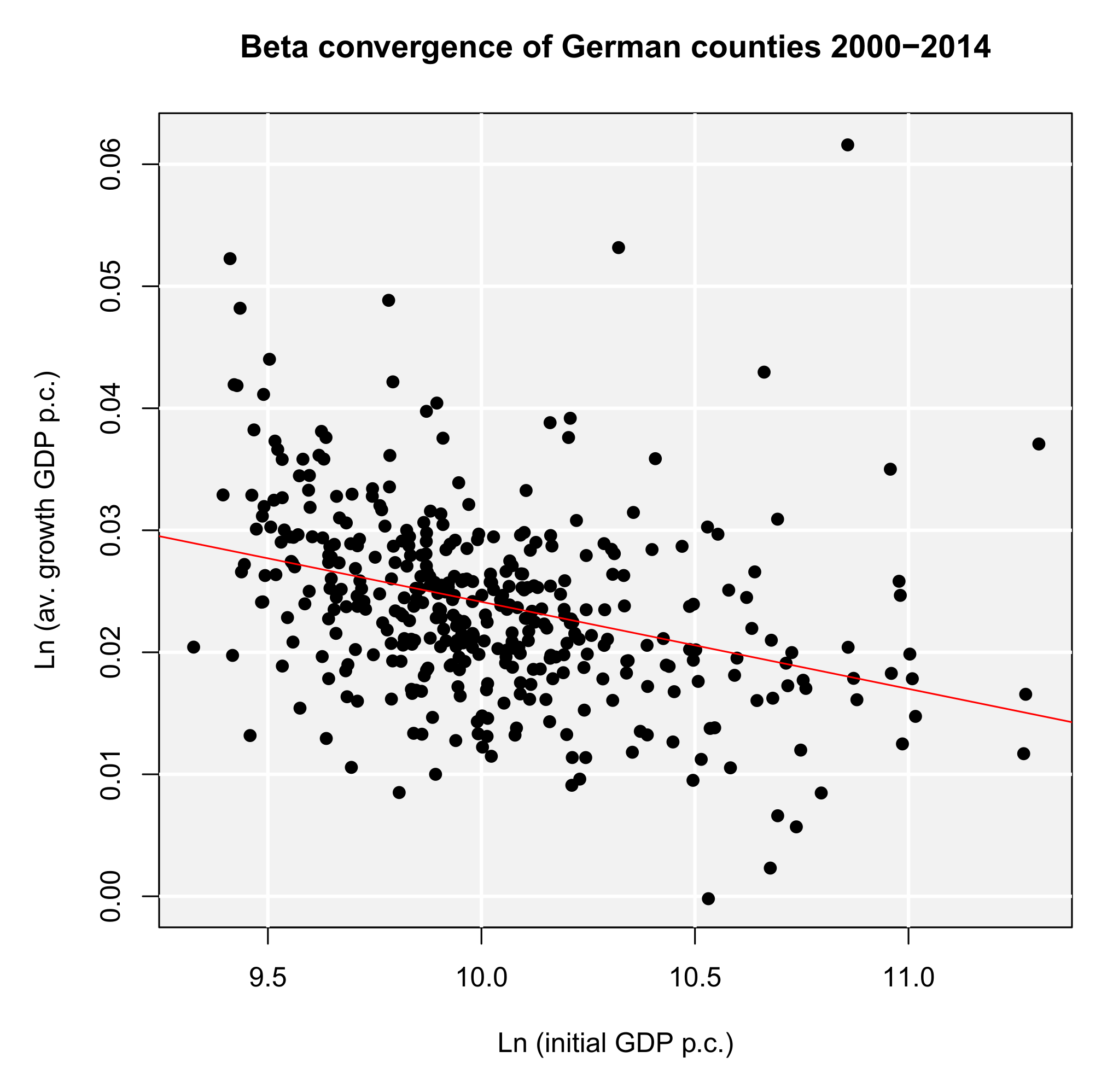 (a) Absolute beta convergence
(a) Absolute beta convergence 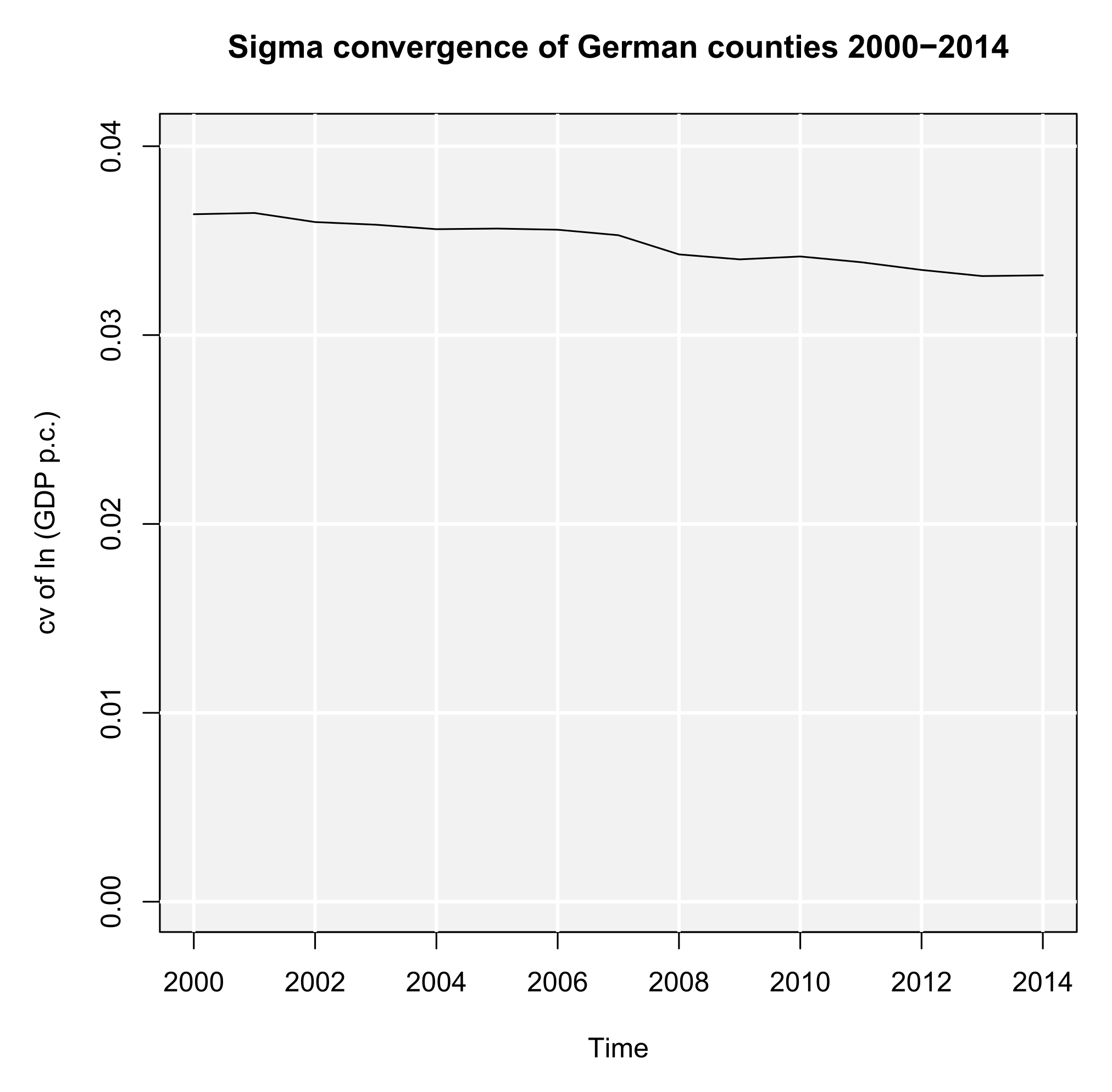 (b) Sigma convergence
(b) Sigma convergence
Remembering German reunification, we want to test if there are average growth differences between West Germany and East Germany (former German Democratic Republic), which leads to conditional beta convergence. The dataset G.regions.emp contains the column regional, where the counties are attributed either to West or East Germany, expressed as character string ("West" or "East"). We need to include our condition into the convergence equation. Thus, we use the REAT function to.dummy() to create dummy variables (1/0) out of (nominal scaled) variables, and add the indicator for West Germany (1, otherwise 0) to our data:
# Creating dummy variables for West/East
# regionaldummies[,1] = East (1/0), regionaldummies[,2] = West (1/0)
G.counties.gdp$West <- regionaldummies[,2]
# Adding the dummy variable for West
Now, we test for conditional beta and sigma convergence, including the condition “West”, again using the rca() function, but without plots and using the standard deviation (default setting) instead of the cv for sigma convergence. This time, we save the results in an object:
G.counties.gdp[55:68], 2014, conditions = G.counties.gdp[c(70)],
sigma.type = "trend")
# condition variable "West" in column 70
# Store results in "converg_results"
The output is:
Absolute Beta Convergence
Model coefficients (Estimation method: OLS)
Estimate Std. Error t value Pr (>|t|)
Alpha 0.0954564 0.0099087 9.634 0.00000000000000000006845
Beta -0.0071323 0.0009885 -7.215 0.00000000000271925822550
Lambda 0.0005113 NA NA NA
Halflife 1355.7282963 NA NA NA
Model summary
Estimate F value df 1 df 2 Pr (>F)
R-Squared 0.1152 52.06 1 400 0.000000000002719
Conditional Beta Convergence
Model coefficients (Estimation method: OLS)
Estimate Std. Error t value Pr (>|t|)
Alpha 0.0754412 0.0102354 7.371 0.0000000000009872
Beta -0.0047020 0.0010517 -4.471 0.0000101720129094
West -0.0053559 0.0009745 -5.496 0.0000000693910790
Lambda 0.0003366 NA NA NA
Halflife 2058.9555949 NA NA NA
Model summary
Estimate F value df 1 df 2 Pr (>F)
R-Squared 0.1774 43.04 2 399 0.00000000000000001192
Sigma convergence (Trend regression)
Estimate Std. Error t value Pr(>|t|)
Intercept 3.895236 0.3267817 11.92 0.00000002264
Time -0.001764 0.0001628 -10.84 0.00000007041
Model summary
Estimate F value df 1 df 2 Pr (>F)
R-Squared 0.9003 117.4 1 13 0.00000007041
In the rca() output, we can compare the results of absolute and conditional beta convergence. In the conditional model, the explained variance increases from R2 ≈ 0.12 to R2 ≈ 0.18, which indicates an increased explanatory power of the model due to the added condition variable. Both models are statistically significant, also the β values are negative and significant (p < 0.001 in both cases). The condition “West” is significant (t ≈-5.50, p < 0.001) and negative, which means that, on average, the GDP per capita in West German counties grew slower than in East Germany. These results seem to support the convergence hypothesis from growth theory, but one should not forget that e.g. political aspects (such as the German and/or EU regional policy) are not considered in this simple analysis.
As we have saved the invisible function output, we can access specific parts of our analysis, such as the regression data for the absolute convergence model:
# All results in list converg_results
# converg_results contains list betaconv (beta convergence results)
# betaconv contains data frame regdata (regression data)
ln_initial ln_growth
1 11.002 0.01997436
2 10.552 0.02980133
3 10.283 0.01794207
4 10.090 0.01763444
5 10.287 0.02361006
...
If we want to look at the single sigma values, we can address them via:
# All results in list converg_results
# converg_results contains list sigmaconv (sigma convergence results)
# sigmaconv contains data frame sigma.trend (sigma values)
years sigma.years
gdp1 2000 0.3646
gdppc2001 2001 0.3662
gdppc2002 2002 0.3618
gdppc2003 2003 0.3606
gdppc2004 2004 0.3592
...
4 Specialization of regions and spatial concentration of industries
4.1 Indicators of regional specialization and industry concentration
Specialization of regions or countries and the spatial concentration of industries or firms are phenomena linked to several research fields in regional economics and economic geography: Specialization is a key point in traditional theories of international trade with respect to comparative advantages (Ricardo, 1821) as well as in the generation of the “New Trade Theory” (introduced by Krugman 1979). Spatial clustering of firms or industries due to agglomeration economies is a perennial issue in all spatial economic fields. It especially reemerged in the context of the “New Economic Geography” (e.g. Krugman 1991; Fujita et al. 2001) as well as through the work of Porter (1990) regarding clusters. The common indicators are broadly discussed in Farhauer, Kröll (2014) or Nakamura, Morrison Paul (2009). For studies comparing some different indicators, see e.g. Goschin et al. (2009); Moga, Constantin (2011); Palan (2017).
When looking at the family of indicators of regional specialization and industry concentration, we have to distinguish between indicators for aggregate data, such as regional employment data, and those requiring individual firm data. The first group, compiled in Table 5, can be differentiated into indicators of specialization and indicators of spatial concentration. As both types of agglomeration are closely linked to each other, so are the corresponding indicators. The empirical basis of all those measures is the employment e in industry i in region j, eij. This employment stock is compared to some reference, mostly including the total employment in region j, ej, and/or the total employment in industry i, ei, as well as the all-over employment e. The individual firm level indicators in Table 6 can be segmented into indicators for agglomeration of one industry due to localization economies and indicators for the coagglomeration of different industries due to urbanization economies.
| Indicator | Specialization of region j | Spatial concentration of industry i |
| Hoover/Balassa | LQij = 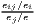 ≡ MRCAij = ≡ MRCAij = 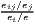 |
|
LQj = 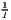 ∑
i=1ILQij ∑
i=1ILQij | LQi = 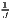 ∑
j=1JLQij ∑
j=1JLQij |
|
| Extensions: | ||
| O’Donoghue-Gleave | SLQij = 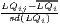 |
|
| Tian | SLLQij = 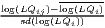 |
|
| Hoen-Oosterhaven | ARCAij = 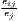 - -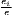 |
|
| Hoover | Hj = 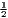 [∑
i=1I| [∑
i=1I|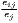 - -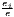 |] |] | Hi = 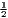 [∑
j=1J| [∑
j=1J|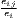 - -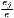 |] |] |
| 0 ≤ Hj ≤ 1 | 0 ≤ Hi ≤ 1 | |
| Gini | Gj = 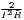 ∑
i=1Iλi(Ri -) ∑
i=1Iλi(Ri -) | Gi = 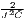 ∑
j=1Jλj(Cj -) ∑
j=1Jλj(Cj -) |
| 0 ≤ Gj ≤ 1 | 0 ≤ Gi ≤ 1 | |
where: Ri = 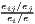 , , | where: Cj = 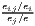 , , |
|
= 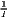 ∑
i=1IRi and ∑
i=1IRi and | = 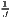 ∑
j=1JCj and ∑
j=1JCj and |
|
| λi = 1,...,I (λi < λi+1) | λj = 1,...,J (λj < λj+1) | |
| Krugman | Kjl = ∑ i=1I|sijs - sils| | Kiu = ∑j=1J|sijc - sujc| |
| (J = 2, I = 2) | 0 ≤ Kjl ≤ 2 | 0 ≤ Kiu ≤ 2 |
where: sijs = 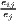 and sils = and sils = 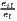 | where: sijc = 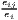 and sujc = and sujc = 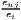 |
|
| Extensions: | ||
| Midelfart et al., | Kj = ∑ i=1I|sijs -ils| | Ki = ∑j=1J|sijc -ujc| |
| Vogiatzoglou | 0 ≤ Kj ≤ 2 | 0 ≤ Ki ≤ 2 |
| (J > 2, I > 2) | where: sijs = 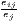 and and | where: sijc = 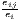 and and |
ils = 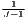 ∑
iJsils, ∑
iJsils, | ujc = 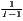 ∑
uIsujc, ∑
uIsujc, |
|
| l≠j | u≠i | |
| Duranton-Puga | RDIj = 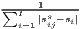 | |
where: sijs = 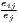 and si = and si = 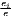 | ||
| Litzenberger-Sternberg | CIij = 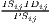 |
|
where ISij = 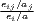 , IDij = , IDij = 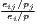 |
||
and PSij = 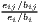 |
||
Notes: eij and eil equal the employment of industry i in regions j and l, respectively, ei is the total employment in industry i, euj ist the employment of industry u in region j, ej is the total employment in region j, e is the total employment in the whole economy, I is the number of industries, J is the number of regions, aj is the area of region j, a is the total area in the whole economy, pj is the population in region j, p is the total population, bij is the number of firms of industry i in region j and bi is the number of firms in industry i.
Compiled from: Farhauer, Kröll (2014); Hoen, Oosterhaven (2006); Hoffmann et al. (2017); Nakamura, Morrison Paul (2009); O’Donoghue, Gleave (2004); Tian (2013); Schätzl (2000); Störmann (2009)
| Indicator | Agglomeration | Coagglomeration |
| Ellison-Glaeser | γi = 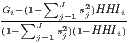 | γc = 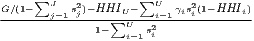 |
| where: Gi = ∑ j=1J(sijc - sj)2, | where: G = ∑j=1J(xj - sj)2, | |
sijc = 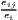 , sj = , sj = 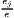 and and | xj = ∑
i=1U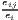 , sj = , sj = 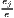 , si = , si = 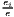 |
|
HHIi = ∑
k=1K(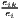 )2 )2 | and HHIU = ∑ i=1Usi2HHIi | |
| z-standardization: | ||
zi = 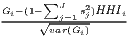 |
||
where: var(Gi) = 2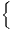 HHIi2 HHIi2 ∑
j=1Jsj2 ∑
j=1Jsj2 |
||
-2 ∑
j=1Jsj3 + (∑j=1Jsj2)2![]](267115x.png) - - |
||
∑
k=1Kzik4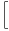 ∑
j=1Jsj2 - 4 ∑j=1Jsj3 ∑
j=1Jsj2 - 4 ∑j=1Jsj3 |
||
+3(∑
j=1Jsj2)2![]](267117x.png) 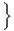 |
||
| Howard et al. | CLab = 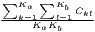 |
|
| XCLab = CLab - CLabRND | ||
| where: Ckl = 1 if firms k and l are located | ||
| in the same region and Ckl = 0 otherwise | ||
Notes: eij is the employment of industry i in region j, ei is the total employment in industry i, ej is the total employment in region j, e is the total employment in the whole economy, eik is the employment of firm k from industry i, k and l are indices for single firms, I is the number of industries, J is the number of regions, U is a subset of all I industries (U ≤ I), K is the number of firms and Ka and Kb are the numbers of firms in industry a and b.
Compiled from: Farhauer, Kröll (2014); Howard et al. (2016); Nakamura, Morrison Paul (2009)
The most popular indicator is the Location Quotient (LQ), which is attributed to Hoover (1936) and mathematically equivalent to the Revealed Comparative Advantage (RCA) index, developed by Balassa (1965) in the context of international trade. The LQ is utilized in many studies (e.g. Bai et al. 2008; Kim 1995) as well as in the OECD Territorial Reviews (OECD, 2019). Following O’Donoghue, Gleave (2004) and Tian (2013), the original formulation can be extended: As the location quotient is not normalized, there is no cut-off value for defining a cluster, which leads to a standardization of the computed values via z-transformation. Hoen, Oosterhaven (2006) developed an additive alternative to the RCA index. The original LQ provides the main mathematical basis for several indicators developed later, such as the spatial Gini coefficients described below.
Some indicators which are known from the context of regional inequality (see Section 2) are also used for the analysis of agglomeration: A modification of the Gini coefficient is used for the spatial concentration of industries as well as regional specialization (e.g. Ceapraz 2008; Wieland, Fuchs 2018). As we can see in the calculation of Ri and Cj, respectively, the spatial Gini coefficient is based on the LQ. Another popular option for analyzing agglomeration is the Hoover coefficient, comparing the structure of an industry/a region to a reference structure of all industries/regions (e.g. Dixon, Freebairn 2009; Jiang et al. 2007). Both indicator types range between zero (no specialization/concentration) and one (total specialization/concentration). Also the Herfindahl-Hirschman index and its derivates are used to measure concentration, specialization and diversification (e.g. Duranton, Puga 2000; Goschin et al. 2009; Lehocký, Rusnák 2016).
Another type of specialization/concentration indicator was introduced by Krugman (1991), originally designed for comparing the specialization of two regions. An extension of this indicator was established by Midelfart-Knarvik et al. (2000) for the comparison of regional specialization/industry concentration with respect to the sum or mean of all regions/industries (furthermore used e.g. by Haas, Südekum 2005; Vogiatzoglou 2006). Unlike the Gini- or Hoover-type measures, the Krugman coefficients range between zero (no specialization/concentration) and two (total specialization/concentration).
The cluster index developed by Litzenberger, Sternberg (2006) goes beyond employment data and includes additional information about the industry-specific firm size, population density and region size. It is composed of three parts: the relative industrial stock with respect to industry i and region j, ISij, the relative industrial density, IDij, and the relative firm size, PSij. All three components are modified location quotients. This is done to control for small and monostructural regions, which are identified as clusters otherwise (which is a problem in the original LQ). The cluster index CIij has a potential range from zero to infinity. This extended indicator is used e.g. by Hoffmann et al. (2017) for the German food processing industry.
The cluster indicators by Ellison, Glaeser (1997) compare the empirical distribution of firms to an arbitrary location pattern where agglomeration economies are absent (often referred to as a dartboard approach). Ellison, Glaeser (1997) differentiate between the clustering of firms from one industry (agglomeration) due to localization economies and the clustering of multiple industries (coagglomeration) due to urbanization economies. Their indices also take into account the industry-specific structure of the firms by including the Herfindahl-Hirschman index, HHIi, for the employment concentration in industry i. This is the reason why individual firm-level data is required for the computation. The Herfindahl-Hirschman indicator is included to control the raw measures of spatial concentration, Gi and G, for firm employment concentration, which occurs especially when there are just a few firms with many employees. The Ellison-Glaeser (EG) index for agglomeration, γi, is designed for identifying the clustering of industry i, while the coagglomeration index, γc aims at the clustering of a set of U industries, where U ≤ I. Values of γ equal to zero imply the absence of agglomeration economies, while values above zero indicate positive effects due to spatial clustering. When γ is negative, firm locations are less spatially concentrated than expected on condition of the dartboard approach, which indicates negative agglomeration economies. The EG index is used in several current regional economic studies (e.g. Dauth et al. 2015, 2018; Yamamura, Goto 2018).
In contrast, Howard et al. (2016) argue that agglomeration economies should not be analyzed regarding employment but the firms itself. Their colocation index, CLab, sums the colocation of Ki and Kq firms from two industries, i and q, controlling for all possible combinations. This colocation measure is compared to a counterfactual location structure constructed via bootstrapping; specifically the arithmetic mean of a number of (e.g. 50) random assignments of the regarded firms to the locations. The value of the resulting excess colocation index, XCLab, ranges between -1 and 1.
4.2 Application in REAT
4.2.1 REAT functions for regional specialization and industry concentration
Table 7 shows the REAT functions for agglomeration measures based on aggregate (employment) data. All functions require at least information about the employment in one or more regions j in one or more industries i, eij. The Herfindahl-Hirschman index (function herf()) for measuring regional diversity is not displayed as it is used exactly in the same way as described in Section 2, replacing xi with eij.
| Indicator | REAT function | Mandatory arguments | Optional arguments | Output |
| Hoover LQ/ | locq() | vectors or single | LQ method, | Single value or |
| Balassa RCA | values of eij and ei, | plot | matrix with LQij | |
| incl. extensions | single values of | |||
| ej and e | ||||
| locq2() | vectors of eij, | normalization, | matrix or data | |
| industry ID i | output type, | frame with I * J | ||
| and region ID j | remove NAs | values of LQij | ||
| Hoover | hoover() | vectors of eij | remove NAs | value: Hj |
| specialization/ | (see Section 2) | and reference | or Hi | |
| concentration | vector ei or ej | |||
| Gini | gini.spec() | vectors eij | plot LC | value: Gj, |
| specialization | and ei | optional: LC plot | ||
| concentration | gini.conc() | vectors eij | plot LC | value: Gi, |
| and ej | optional: LC plot | |||
| Krugman | krugman.spec() | vectors eij | value: Kjl | |
| specialization | (regions j and l) | and eil | ||
| krugman.conc2() | vector eij and matrix | value: Kj | ||
| (all J regions) | or data frame eil | |||
| concentration | krugman.conc() | vectors eij | value: Kiu | |
| (industries i and u) | and euj | |||
| krugman.conc2() | vector eij and matrix | value: Ki | ||
| (all I industries) | or data frame euj | |||
| All at once: | ||||
| specialization | spec() | vectors of eij, | remove NAs | matrix with Hj, Gj |
| industry ID i | and Kj (columns) | |||
| and region ID j | for J regions (rows) | |||
| concentration | conc() | vectors of eij, | remove NAs | matrix with Hi, Gi |
| industry ID i | and Ki (columns) | |||
| and region ID j | for I industries (rows) | |||
| Duranton- | durpug() | vectors eij | value: RDIj | |
| Puga | and ei | |||
| Litzenberger- | litzenberger() | single values of | value: CIij | |
| Sternberg | eij, ei, aj, a, | |||
| pj, p, bij and bi | ||||
| litzenberger2() | vectors of eij, | output type, | matrix or data | |
| industry ID i, | remove NAs | frame with I * J | ||
| region ID j, | values of CIij | |||
| aj, pj and bij | ||||
Source: own compilation.
Location quotients for one region and one or more industries are computed by the function locq(), including the option for an additive indicator instead of the multiplicative. When calculating the LQ for a set of J regions and I industries, one can use function locq2(), which is a kind of batch processing extension of locq(). As the dimension of the Litzenberger-Sternberg cluster index is the same as in the LQ (a single value for each combination of region j and industry i), the related functions litzenberger() and litzenberger2() work in the same way. When using locq2() or litzenberger2(), the user may choose the type of function output: either a matrix with I columns and J rows or a data frame with I * J rows.
The Hoover-, Gini- and Krugman-type indicators require the same kind of input data. The hoover() function was already explained in Section 2, as it can be also used for measuring spatial concentration of industries or the specialization of regions with all-over employment vectors, ei and ej, respectively, as reference distributions. The spatial Gini coefficients are available through functions gini.spec() for regional specialization and gini.conc() for spatial concentration. The Krugman coefficients are divided into functions for the comparison of two regions/industries (krugman.spec() and krugman.conc(), respectively) and for applying all regions/industries as reference (krugman.spec2() and krugman.conc2(), respectively). The functions spec() and conc() are wrapper functions providing a convenient way to compute Hoover, Gini and Krugman coefficients of a given set of J regions and I industries at once, e.g. originating from official statistics on regional employment.
| Indicator | REAT function | Mandatory arguments | Optional arguments | Output |
| Ellison-Glaeser | ellison.a() | vectors of eik, ej | visible: value γi, | |
| agglomeration | and region ID j | invisible: matrix with γi, | ||
| Gi, zi, Ki and HHIi | ||||
| ellison.a2() | vectors eik, | visible: values γi, | ||
| industry ID i and | invisible: matrix with γi, | |||
| region ID j | Gi, zi, Ki and HHIi, | |||
| for I industries (rows) | ||||
| coagglomeration | ellison.c() | vectors eik, | vectors ej and | value: γc |
| industry ID i and | U industries | |||
| region ID j | ||||
| ellison.c2() | vectors eik, | vector ej | matrix with γc for | |
| industry ID i and | I * I - I industry | |||
| region ID j | combinations (rows) | |||
| Howard et al. | howard.cl() | firm ID k, | value: CLab | |
| colocation | industry ID i, | |||
| and region ID j, | ||||
| industries a and b | ||||
| excess | howard.xcl() | firm ID k, | value: XCLab | |
| colocation | industry ID i | |||
| and region ID j, | ||||
| industries a and b, | ||||
| no. of samples | ||||
| howard.xcl2() | firm ID k, | matrix with XCLab for | ||
| industry ID i | I * I - I industry | |||
| and region ID j | combinations (rows) | |||
Source: own compilation.
Table 8 shows the functions operating on the level of individual firm data. The Ellison-Glaeser (EG) indices are available through the functions ellison.a() (agglomeration index for industry i) and ellison.a2() (agglomeration indices for I industries) as well as ellison.c() (coagglomeration index for U industries) and ellison.c2() (coagglomeration indices for I * I - I industry combinations). All functions require the firm size (e.g. no. of employees) for the k-th firm from industry i (numeric vector) and the region j the firm is located in. The functions incorporating more than one industry (all except for ellison.a()) require a vector containing the industry i. The data could e.g. be stored in a data frame with at least three columns (firm size, region, industry). Like some of the convergence functions (see Section 3), the EG agglomeration index functions in REAT also distinguish between a visible and an invisible output: ellison.a() and ellison.a2() show the value(s) auf γi but return an invisible matrix including the raw measure of concentration (Gi), the z-standardized results (zi) and the related Herfindahl-Hirschman index for industry-specific firm concentration (HHIi) as well as the number of firms in industry i (Ki).
The Howard-Newman-Tarp coagglomeration measure is distributed over the functions howard.cl() (calculation of the colocation index for one pair of industries a and b), howard.xcl() (calculation of the excess colocation index for industries a and b) and howard.xcl2() (calculation of the excess colocation index for I * I - I combinations of I industries). As this cluster index works with firms instead of employment, we only need a vector containing the IDs of the firms k, the corresponding industry i and the region j where the firm is located. When calculating this measure for one pair of industries, the user must state the IDs of industries a and b. Note that calculation time for this index increases heavily with the number of firms and/or industries.
4.2.2 Application example 1: Regional specialization of Göttingen
We use the German classification of economic activities (WZ2008) on the level of 21 sections (A-U) for the classification of industries in the following examples (see Table 9).
WZ2008 | |
| Code | Title |
| A | Agriculture, forestry and fishing |
| B | Mining and quarrying |
| C | Manufacturing |
| D | Electricity, gas, steam and air conditioning supply |
| E | Water supply; sewerage, waste management and remediation activities |
| F | Construction |
| G | Wholesale and retail trade; repair of motor vehicles and motorcycles |
| H | Transportation and storage |
| I | Accommodation and food service activities |
| J | Information and communication |
| K | Financial and insurance activities |
| L | Real estate activities |
| M | Professional, scientific and technical activities |
| N | Administrative and support service activities |
| O | Public administration and defence; compulsory social security |
| P | Education |
| Q | Human health and social work activities |
| R | Arts, entertainment and recreation |
| S | Other service activities |
| T | Activities of households as employers; undifferentiated goods-and services-producing |
| activities of households for own use | |
| U | Activities of extraterritorial organisations and bodies |
Source: own compilation based on Statistisches Bundesamt (2008).
Starting with a simple example, we analyze the regional specialization of Göttingen, a city with a population of about 134,000 in Niedersachsen, Germany. The example dataset Goettingen, which is included in REAT, contains the dependent employees in Göttingen and Germany for 2008 to 2017 in industries A to R (rows 2 to 16; row 1 contains the all-over employment). First, we load the data:
Using the REAT function locq(), we calculate a location quotient for Göttingen with respect to the manufacturing industry (”Verarbeitendes Gewerbe”), which is represented by letter C:
Goettingen$BRD2017[4], Goettingen$BRD2017[1])
# Industry: manufacturing (letter C) in row 4
# row 1 = all-over employment
[1] 0.5369
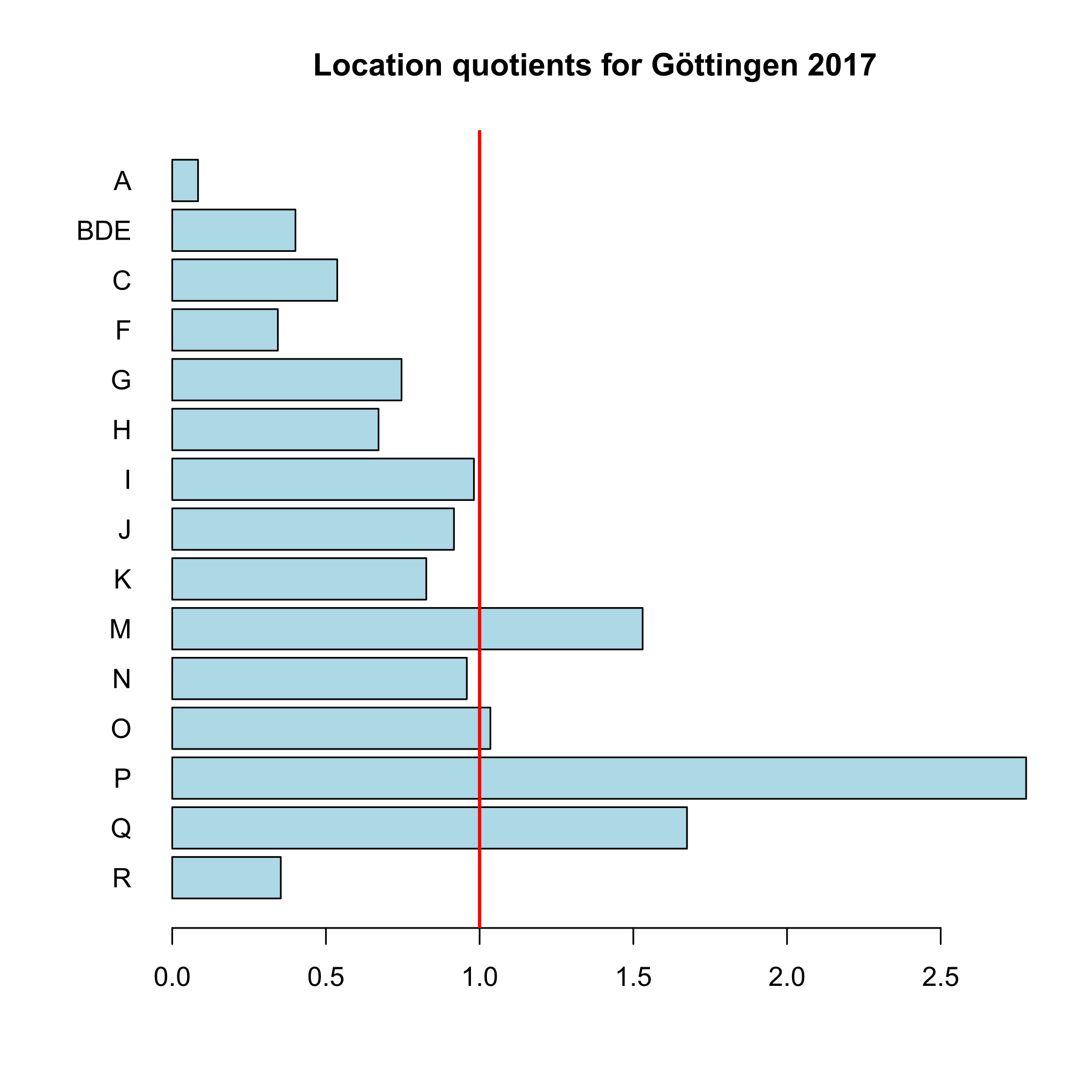
The output is simply the LQ value (LQij, where i is manufacturing and j is Göttingen). We see that the LQ is very low, indicating that manufacturing is underrepresented in Göttingen as compared to Germany. Now, we calculate LQ values for all industries (A-R), including a simple plot (function argument plot.results = TRUE):
Goettingen$BRD2017[2:16], Goettingen$BRD2017[1],
industry.names = Goettingen$WZ2008_Code[2:16], plot.results = TRUE,
plot.title = "Location quotients for Göttingen 2017")
# all industries (rows 2-16 in the dataset)
The output is a matrix with one row for each industry:
I = 15 industries
LQ
A 0.08407652
BDE 0.40085663
C 0.53687366
F 0.34366928
G 0.74603541
H 0.67117311
I 0.98141916
J 0.91654277
K 0.82650178
M 1.53027645
N 0.95843423
O 1.03509027
P 2.77790858
Q 1.67459967
R 0.35317012
The result is plotted in Figure 3. The function plots a vertical line at LQij = 1 automatically. This is the (only) reference value for the LQ. It indicates a stock of the related industry equal to the whole economy. The highest LQ values can be found for the industries with letters P (education) and Q (health). This is because Göttingen is mainly characterized by a large university (about 30,000 students) with a university hospital with about 7,000 employees.
Now, we want to measure the specialization of Göttingen with a single indicator. First, we simply use the Herfindahl-Hirschman coefficient for both Göttingen and Germany using the function herf():
[1] 0.127314
herf(Goettingen$BRD2017[2:16])
[1] 0.1104567
The HHI for Göttingen is slightly larger than for Germany, which indicates a higher specialization (or lower economic diversity) of the region. To combine this information in one indicator, we calculate the Hoover coefficient of specialization using the function hoover(), where the reference distribution is the German industry structure:
[1] 0.2254234
We finish our analysis of Göttingen’s regional specialization by calculating both the Gini and the Krugman coefficient of regional specialization with the same data, using the REAT functions gini.spec() and krugman.spec(), respectively. Note that, here, we use the Krugman coefficient to compare the industry structure of Göttingen to the structure of whole Germany (instead of another region within the country, for which this coefficient was originally formulated):
[1] 0.359852
krugman.spec(Goettingen$Goettingen2017[2:16], Goettingen$BRD2017[2:16])
[1] 0.4508469
There seems to be some specialization in Göttingen, but, unfortunately, we do not have any real reference value to interpret the results.
4.2.3 Application example 2: Identifying clusters in Germany using aggregate data
In this example, we will compute indicators of regional specialization and industry concentration for a set of J regions and I industries at once. We load the included test dataset G.regions.industries containing employment and firms on the level of I = 17 industries (WZ2008 codes B-S) and J = 16 regions (“Bundesländer”) in Germany:
The number of employees in the column emp_all includes dependent employees and self-employed persons. The classification code of industries (see Table 9) can be found in column ind_code, while the region code (abbreviation of the region’s official name) is in column region_code. First, we want to detect the spatial concentration of the 17 industries in Germany by calculating Hoover, Gini and Krugman coefficients for all industries at once, applying the REAT function conc() which is a wrapper function for the mentioned indicators. We save our output in the matrix object conc_i:
industry.id = G.regions.industries$ind_code,
region.id = G.regions.industries$region_code)
The output is:
I = 17 industries, J = 16 regions
H i G i K i
WZ08-B 0.22959050 0.42334831 0.45675385
WZ08-C 0.09933363 0.17047620 0.26813759
WZ08-D 0.07754576 0.12509360 0.16260016
WZ08-E 0.11972072 0.16742909 0.20369011
WZ08-F 0.07676634 0.15357575 0.16996098
WZ08-G 0.03034962 0.05471323 0.07977056
WZ08-H 0.06006957 0.11921850 0.10076748
WZ08-I 0.05177262 0.09939075 0.11450791
WZ08-J 0.10230712 0.22605802 0.24450967
WZ08-K 0.08982871 0.17610712 0.20565974
WZ08-L 0.09798632 0.16784764 0.17472656
WZ08-M 0.06490185 0.14760918 0.14931991
WZ08-N 0.06714816 0.08575299 0.09053327
WZ08-P 0.03019678 0.05053848 0.07043586
WZ08-Q 0.04679962 0.06170335 0.06406058
WZ08-R 0.09424708 0.16748405 0.17023603
WZ08-S 0.04507988 0.07246697 0.06441360
The function returns a matrix with 17 rows (one for each industry) and three columns: H i is the Hoover coefficient, G i is the Gini coefficient and K i is the Krugman coefficient for industry i. We cannot interpret or compare all of these results, but we may pick out some findings: The strongest spatial concentration is found with respect to mining and quarrying (WZ08-B), no matter which indicator is regarded, which may be interpreted with “natural advantages” due to the spatial distribution of mineral resources in Germany. Services (such as retailing) as well as education and health are least concentrated, as these industries are bound to regional demand and/or their locations are regulated by policy and planning authorities.
At a first glance, the three indicators seem to produce similar results. Now, we want to test the similarity between Hoover, Gini and Krugman coefficients of concentration. As we saved our result matrix, we now calculate Pearson correlation coefficients (r) for each pair of indicators using the basic R function cor(), which is implemented in the stats package (included automatically in any R release). The function is applied to the three columns of conc_i, producing a 3 * 3 correlation matrix:
H i G i K i
H i 1.0000000 0.9676518 0.9527747
G i 0.9676518 1.0000000 0.9681770
K i 0.9527747 0.9681770 1.0000000
As we can see, each combination of the three indicators shows a strong positive correlation (Hi vs. Gi: r ≈ 0.97, Hi vs. Ki: r ≈ 0.95, Gi vs. Ki: r ≈ 0.97). At least in this context, we may conclude that these indicators are interchangeable. However, we have to recognize that the analysis presented here is on a large-scale regional level (German “Bundesländer”) and all of the mentioned indicators are affected by the modifiable areal unit problem, which means that the results depend on the aggregation unit in the analysis (see e.g. Dapena et al. 2016 for a discussion of this effect).
Now, we do exactly the same with respect to regional specialization of the 16 regions, using the same data. Analogously, we use the wrapper function spec() for calculating Hoover, Gini and Krugman coefficients of regional specialization, also saving the resulting matrix:
industry.id = G.regions.industries$ind_code,
region.id = G.regions.industries$region_code)
The output is:
I = 17 industries, J = 16 regions
H j G j K j
BB 0.11530353 0.20632682 0.18555259
BE 0.17891265 0.29040841 0.34552331
BW 0.08024011 0.10300695 0.22675612
BY 0.05008135 0.07659148 0.16019603
HB 0.09502615 0.18563500 0.17467291
HE 0.05494422 0.12160142 0.11282696
HH 0.16413456 0.22616814 0.33190321
MV 0.13270849 0.18974606 0.22056868
NI 0.03772799 0.08237225 0.07972852
NW 0.02940091 0.05997505 0.07181569
RP 0.04793147 0.07432361 0.12036513
SH 0.08901907 0.11384295 0.15994524
SL 0.05726933 0.11921727 0.15071159
SN 0.05400855 0.10643512 0.10341280
ST 0.08821395 0.21120287 0.15280711
TH 0.08234046 0.13902924 0.17720208
The strongest specialization can be found in the city states Berlin (BE) and Hamburg (HH), while Niedersachsen (NI) and Nordrhein-Westfalen (NW) show the lowest values in all three indicators. As already mentioned in the concentration example, we have to remember the large-scale aggregation unit. If we used smaller scale units (e.g. counties like in Section 3.2.2), our results would surely be more differentiated. Again, we check the correlation between the indicators:
H j G j K j
H j 1.0000000 0.9179127 0.9322604
G j 0.9179127 1.0000000 0.7907841
K j 0.9322604 0.7907841 1.0000000
Again, we find a strong positive correlation between the Hoover coefficient and both Gini and Krugman coefficient (Hj vs. Gj: r ≈ 0.92, Hj vs. Kj: r ≈ 0.93), while the third Pearson correlation coefficient is a little lower, but still showing the same direction (Gj vs. Kj: r ≈ 0.79).
Now we check for clusters in a combination of a specific industry and a specific region. First, we calculate location quotients for the dataset G.regions.industries using the REAT function locq2(). Here, the optional function argument LQ.norm could be used for computing z-standardized location quotients according to O’Donoghue, Gleave (2004) (LQ.norm = "OG") or z-standardized values of the natural-logged LQs according to Tian (2013) (LQ.norm = "T"). However, we produce the original LQs, since we need exactly the same columns as in the examples above:
G.regions.industries$ind_code, G.regions.industries$region_code)
The output is a matrix with J rows and I columns:
I = 17 industries, J = 16 regions
BB BE BW BY HB HE
WZ08-B 2.5314363 0.04030901 0.6607950 0.8078054 0.0000000 0.3735773
WZ08-C 0.6857231 0.37224900 1.3968652 1.1902785 0.7863570 0.8580352
WZ08-D 1.1736475 0.46721079 1.0861988 0.8343784 0.9179718 0.9627955
WZ08-E 1.7945685 1.30128835 0.5896526 0.7137388 1.2393228 0.8532203
WZ08-F 1.5997778 0.77160121 0.9070096 1.0280409 0.6212923 0.8927681
WZ08-G 0.9550127 0.83133221 0.9492523 0.9879826 0.9013193 1.0006321
WZ08-H 1.3212794 0.87982228 0.8189666 0.8664163 1.7692815 1.2208728
WZ08-I 1.0379426 1.35561299 0.9132949 1.0390886 0.9904308 0.9571339
WZ08-J 0.5625876 1.78334039 1.0316114 1.1550764 1.0577107 1.1407078
WZ08-K 0.6529329 0.76630600 0.9329930 1.1058890 0.7825178 1.6710583
WZ08-L 1.1088846 2.13220960 0.7310014 0.8633894 1.3254723 1.1132939
WZ08-M 0.7366238 1.39880205 1.0337139 1.0265993 1.1202532 1.1457770
WZ08-N 1.2571301 1.24261162 0.7977054 0.8486971 1.2938161 1.0525912
WZ08-P 0.9052976 1.38842157 0.9649289 0.9252245 1.0563169 1.0085207
WZ08-Q 1.1540423 1.09329902 0.8695241 0.9079679 0.9544891 0.8980680
WZ08-R 1.0656945 2.55595102 0.8518192 0.8220540 1.3196613 0.8651451
WZ08-S 1.1409373 1.32596177 0.8626829 0.9092125 1.1396616 1.0528184
HH MV NI NW RP SH
WZ08-B 0.6029388 0.6235796 1.4987086 1.4595767 1.0371236 0.5078145
WZ08-C 0.4781934 0.6230156 0.9512438 0.9312325 1.0822678 0.7082513
WZ08-D 0.4332870 1.0118838 0.9932719 1.2139740 0.9349679 1.1248685
WZ08-E 1.1442005 1.5642257 1.0645497 1.0408356 0.9886860 1.0707585
WZ08-F 0.5432163 1.2716537 1.0969756 0.8735506 1.1134885 1.1043449
WZ08-G 1.0654315 0.9485377 1.0758977 1.0612190 1.0111274 1.2456100
WZ08-H 1.4958610 1.1243732 1.0409143 0.9961224 0.9633972 1.0112557
WZ08-I 1.0634066 1.7574637 1.0227196 0.8750205 1.1121264 1.2483966
WZ08-J 1.9266913 0.4751473 0.6716376 0.9830609 0.8122058 0.7496925
WZ08-K 1.5175078 0.5383900 0.9108456 1.0205798 0.8879292 0.8355178
WZ08-L 1.5871838 1.3034074 0.8040270 0.9928161 0.7774500 1.1980553
WZ08-M 1.6293913 0.6897571 0.8693026 1.0366589 0.7764558 0.7905498
WZ08-N 1.2530608 1.2484353 0.9675147 1.0659893 0.8026181 0.9727871
WZ08-P 0.9422739 0.9966228 1.0888054 0.9846351 1.0976178 0.9540262
WZ08-Q 0.8564604 1.2893168 1.0728412 1.0595648 1.0418460 1.1662290
WZ08-R 1.4914564 1.0500685 0.9204586 0.9611539 0.8498053 1.0418794
WZ08-S 0.8055128 1.1158184 0.9965451 1.0283571 1.1658852 1.1455178
SL SN ST TH
WZ08-B 0.2826284 1.2746172 2.4654331 0.7140637
WZ08-C 1.1752810 0.9867417 0.9297172 1.1849897
WZ08-D 1.1465539 1.0637093 1.2642787 0.8607578
WZ08-E 0.9555581 1.4457486 1.8251853 1.6042935
WZ08-F 0.9016858 1.3794286 1.4104724 1.3481005
WZ08-G 1.0370901 0.8787739 0.9172598 0.8661184
WZ08-H 0.8851047 1.0476688 1.2012430 0.8944907
WZ08-I 0.9111877 0.9496370 0.9020582 0.8644257
WZ08-J 0.7133587 0.7717704 0.4874344 0.6869177
WZ08-K 1.0082983 0.6620719 0.6133933 0.6316347
WZ08-L 0.7018816 1.1395422 1.0111694 0.8511896
WZ08-M 0.8060753 0.8459317 0.6627301 0.6814339
WZ08-N 1.0751749 1.1656467 1.2796548 1.1093251
WZ08-P 0.9147874 0.9658590 0.9798932 0.9710576
WZ08-Q 1.0760969 1.0475595 1.1401680 1.0628602
WZ08-R 0.7631263 1.1419135 0.8329295 0.8582919
WZ08-S 0.8840741 0.9774726 0.9257397 1.0923137
These I * J = 17 * 16 = 272 coefficients are too much information. Thus, we calculate them again using the optional argument LQ.output = "df", which produces a data frame with I * J rows and three columns (j_region: ID of region j, i_industry: ID of industry i and LQ: location quotient LQij). We save the results in the object lqs:
G.regions.industries$ind_code, G.regions.industries$region_code,
LQ.output = "df")
As we forego an inspection of these singe values, the results are not displayed here. Instead, we only deal with the five highest LQs in our results (the “top five”). We sort the resulting data frame decreasing and take a look at the first five rows:
# Sort decreasing by size of LQ
lqs_sort[1:5,]
j_region i_industry LQ
33 BE WZ08-R 2.555951
1 BB WZ08-B 2.531436
239 ST WZ08-B 2.465433
28 BE WZ08-L 2.132210
111 HH WZ08-J 1.926691
The highest LQ is found for the arts, entertainment, and recreation sector (WZ08-R) in the German capital Berlin. Note that this result is congruent with several studies about the “creative class”, showing a large stock of “creative” employment in Berlin (e.g. Martin 2015). We also find a strong concentration of mining and quarrying in two Eastern regions, Brandenburg and Sachsen-Anhalt. Note that the LQ is a relative measure with respect to the total regional employment as well as the total industry-specific employment and the employment in the whole economy, not considering other aspects of industry or spatial structure.
These deficiencies should be overcome with the Litzenberger-Sternberg cluster index, also taking into account area, population and firm size. This additional data is also included in our current dataset (columns area_sqkm, pop and firms). The functions litzenberger() and litzenberger2() work equivalently to locq() and locq2(). To compute cluster indices for all I * J combinations, we use the function litzenberger2():
G.regions.industries$ind_code, G.regions.industries$region_code,
G.regions.industries$area_sqkm, G.regions.industries$pop,
G.regions.industries$firms)
Like in locq2(), the default output is a matrix with I rows and J columns:
I = 17 industries, J = 16 regions
BB BE BW BY HB HE
WZ08-B 0.5736692 0.05611505 0.8041813 1.1073446 NaN 0.4745084
WZ08-C 0.1610679 3.24717820 2.6250805 1.2043415 5.119669 1.0603087
WZ08-D 0.2213627 1.37720778 1.7043505 1.4178208 4.172162 0.8541359
WZ08-E 0.8810260 10.14891585 0.8235517 0.6890213 6.705744 1.1427285
WZ08-F 0.7142888 11.36434353 1.2372108 0.9442221 3.498921 1.1225087
WZ08-G 0.2707787 12.10626625 1.3903532 0.9404677 7.136205 1.3361060
WZ08-H 0.4386878 13.26265081 1.0955747 0.7982074 22.656924 1.8358272
WZ08-I 0.2672336 26.60020727 1.4098657 0.9633029 8.481338 1.2880210
WZ08-J 0.1130326 59.24931837 1.4342037 1.2393579 8.683998 1.9024826
WZ08-K 0.1524825 10.28664194 1.4774980 1.1692461 6.650213 2.4739044
WZ08-L 0.2564814 56.65943460 0.9594093 0.8695636 11.839900 1.6099929
WZ08-M 0.1685895 39.30149403 1.5306799 1.0110472 9.410498 1.7302434
WZ08-N 0.4232166 26.91532975 1.0228326 0.7471872 10.796027 1.5265846
WZ08-P 0.2043023 25.30839556 1.3656409 0.9509028 7.322709 1.4627871
WZ08-Q 0.3445630 21.86956483 1.1770297 0.7873877 7.850886 1.2163624
WZ08-R 0.2450932 104.73565741 1.0839767 0.7821779 10.555369 1.0489672
WZ08-S 0.2891132 24.71310833 1.3435576 0.9594882 9.893688 1.5421903
HH MV NI NW RP SH
WZ08-B 2.319611 0.16000177 1.5004530 2.074735 1.1951266 0.3119091
WZ08-C 4.000104 0.11993714 0.5036838 2.010757 0.9646351 0.4008598
WZ08-D 1.679371 0.20954802 0.8848956 2.001708 0.6016715 1.2989105
WZ08-E 11.129156 0.44055556 0.6476797 1.915196 0.8616891 0.8101087
WZ08-F 5.526083 0.45291220 0.6276791 1.656384 0.8973162 0.8055662
WZ08-G 15.627090 0.22665565 0.6898359 2.377365 0.8115817 0.9008287
WZ08-H 44.371836 0.32192237 0.6420146 1.980491 0.7087341 0.7205961
WZ08-I 14.795885 0.59842705 0.6335126 1.731963 1.0572996 1.0361389
WZ08-J 59.720584 0.05895184 0.2905769 2.139796 0.5142953 0.4427180
WZ08-K 26.189623 0.12112900 0.5648050 1.953963 0.7104929 0.5758818
WZ08-L 33.175443 0.25167830 0.5228248 2.223854 0.5349641 0.8587588
WZ08-M 44.433527 0.11657637 0.4440959 2.297308 0.4961611 0.4456119
WZ08-N 23.255195 0.31231467 0.5271293 2.413351 0.5537510 0.7348068
WZ08-P 14.294075 0.24008982 0.7203953 2.022971 0.9704975 0.6937792
WZ08-Q 13.211918 0.38626491 0.6877487 2.260518 0.7770980 0.8426253
WZ08-R 44.256214 0.20066782 0.4508862 2.190752 0.5287290 0.6694273
WZ08-S 14.195156 0.27631480 0.5364848 1.941470 0.7996291 0.9238816
SL SN ST TH
WZ08-B 0.3673090 1.1179110 1.49064630 0.4562730
WZ08-C 1.8348713 1.0311722 0.32128528 0.7892360
WZ08-D 0.9643263 0.4534029 0.29391783 0.2086042
WZ08-E 1.9939461 1.5554125 1.09973945 1.1815726
WZ08-F 1.3245152 1.8167263 0.68075807 1.0313749
WZ08-G 1.7528078 0.7644695 0.31005922 0.4313306
WZ08-H 1.1099151 0.9297053 0.42973342 0.4881643
WZ08-I 1.7871163 0.7119567 0.29998391 0.4012910
WZ08-J 0.8984679 0.4927030 0.08046178 0.2087174
WZ08-K 1.5505928 0.5980588 0.21942805 0.3160432
WZ08-L 0.8170723 0.8226773 0.21044244 0.2886068
WZ08-M 1.0137151 0.6489868 0.15797219 0.2493458
WZ08-N 1.3940298 1.2492658 0.42285503 0.5935329
WZ08-P 1.2331390 0.7800531 0.31406013 0.4389675
WZ08-Q 1.8551266 1.0749000 0.48353914 0.5854787
WZ08-R 0.8477702 0.8666478 0.21562997 0.2919300
WZ08-S 1.6138955 0.8600519 0.34624522 0.5369766
Note that there is a value equal to NaN, which means “not a number”, due to a division by zero; this is because there is no mining and quarrying (WZ08-B) in Bremen (HB). However, we take a look at the “top five” again:
G.regions.industries$ind_code, G.regions.industries$region_code,
G.regions.industries$area_sqkm, G.regions.industries$pop,
G.regions.industries$firms, CI.output = "df")
lss_sort <- lss[order(lss$CI, decreasing = TRUE),]
lss_sort[1:5,]
j_region i_industry CI
33 BE WZ08-R 104.73566
111 HH WZ08-J 59.72058
26 BE WZ08-J 59.24932
28 BE WZ08-L 56.65943
114 HH WZ08-M 44.43353
Again, we find the largest cluster value for the arts and entertainment sector in Berlin. Also the other four highest indicators are discovered in the largest city states Berlin and Hamburg, especially with respect to the information and communication industry (WZ08-J) and other knowledge-intensive services. Obviously, the results of the Litzenberger-Sternberg index differ in a noticeable way from those of the LQ, which can be attributed to the consideration of other spatial aspects, especially controlling for the size of the regions.
4.2.4 Application example 3: Identifying clusters using micro-data
In our last example about agglomerations, we use the Ellison-Glaeser indices and the Howard-Newman-Tarp colocation index, which both require individual firm data. As this kind of micro-data is sensitive and, of course, not available in official statistics, we have to use fictional data from the textbook by Farhauer, Kröll (2014).
At first, we compute the Ellison-Glaeser agglomeration index for one industry i, γi. We use the REAT function ellison.a(), which is designed for this purpose and requires three vectors: the size (employment) of firm k, eik, the IDs of the regions j each firm is located in, and the total regional employment, ej. The numerical example in Farhauer, Kröll (2014), Table 14.11, contains ten firms in three regions (Wien, Linz, and Graz). We simply compile the data from the original table into separate vectors:
"Linz", "Linz", "Linz", "Graz")
# regions (Austrian cities)
emp_firm <- c(200,650,12000,100,50,16000,13000,1500,1500,25000)
# employment of the ten firms
emp_region <- c(500000,400000,100000)
# employment of the three regions
Now, we apply ellison.a() to this data:
[1] 0.05990628
The EG agglomeration index of γi ≈ 0.06, which is, by the way, the same result as in the textbook, indicates a stronger clustering than expected from a dartboard approach. Since this data is fictional, we refrain from interpreting this result.
The REAT package contains the dataset FK2014_EGC, which is compiled from the numerical example in Farhauer, Kröll (2014), Tables 14.14 to 14.17. There are k = 42 firms from I = 4 industries (clothing trade, forestry, textiles dyeing and textiles trade) in J = 3 regions (1, 2 and 3). We load this example data:
We compute γi for all industries in the dataset. This can be done with the function ellison.a2(), which requires vectors containing the size of firm k, the corresponding industry i, and region j. We save the results in the object ega:
FK2014_EGC$region)
Here, we see the output of the function:
K = 42 firms, I = 4 industries, J = 3 regions
Gamma i
Clothing trade -0.09379384
Forestry 0.16838003
Textiles dyeing -0.08012539
Textiles trade -0.13040134
We see a strong clustering of the forestry industry, which is attributed to localization economies, but spatial avoidance in the three other industries. The visible output of ellison.a2() contains the γi values only, but the invisible matrix output also includes the other information referring to the EG agglomeration index:
Gamma i G i z i K i HHI i
Clothing trade -0.09379384 0.017909653 -0.5025978 11 0.13124350
Forestry 0.16838003 0.088262934 1.3660878 13 0.09240553
Textiles dyeing -0.08012539 0.027764811 -0.3801644 9 0.14559983
Textiles trade -0.13040134 0.002734966 -0.7663541 9 0.12208059
When looking at the forestry industry, we also see a high standardized value (zi ≈ 1.37) and a relatively low firm concentration (HHIi ≈ 0.09).
In the next step, we compute the EG coagglomeration index, γc, for the same data using the function ellison.c(). This function requires the same information as ellison.a2() plus the total employment in the regarded regions (column emp_region):
FK2014_EGC$region, FK2014_EGC$emp_region)
[1] 12.0729
Congruent with the calculation in Farhauer, Kröll (2014), the function returns γc ≈ 12.07. This value is very large, which indicates urbanization economies in this fictional example.
If we want to analyze the coagglomeration of industry pairs instead, we may use the function ellison.c2(), which requires the same data:
FK2014_EGC$region, FK2014_EGC$emp_region)
The output is a matrix with I * I - I rows (one for each industry pair, omitting the combination of the same industry i):
K = 42 firms, I = 4 industries, J = 3 regions
Gamma c
Forestry-Clothing trade 1.382257
Textiles dyeing-Clothing trade 2.465609
Textiles trade-Clothing trade 2.067766
Clothing trade-Forestry 1.382257
Textiles dyeing-Forestry 1.570292
Textiles trade-Forestry 1.336020
Clothing trade-Textiles dyeing 2.465609
Forestry-Textiles dyeing 1.570292
Textiles trade-Textiles dyeing 2.294259
Clothing trade-Textiles trade 2.067766
Forestry-Textiles trade 1.336020
Textiles dyeing-Textiles trade 2.294259
If we want to focus on firm numbers instead of employment size, we may compute the Howard-Newman-Tarp excess colocation index, which is included in REAT through the functions howard.cl() for one colocation index for one pair of industries, howard.xcl() for the corresponding excess colocation index and howard.xcl2() for all combinations of I * I industries. Subsequent to the numerical example above, we calculate XCLab for all industry pairs in the dataset FK2014_EGC, where the firm ID of k is stored in the column firm:
FK2014_EGC$region)
# this takes some seconds
The output has the same structure as the output from ellison.c2():
K = 42 firms, I = 4 industries, J = 3 regions
XCL
Forestry-Clothing trade 0.01902098
Textiles dyeing-Clothing trade 0.02909091
Textiles trade-Clothing trade 0.02020202
Clothing trade-Forestry 0.02377622
Textiles dyeing-Forestry 0.03282051
Textiles trade-Forestry 0.03589744
Clothing trade-Textiles dyeing 0.02707071
Forestry-Textiles dyeing 0.02666667
Textiles trade-Textiles dyeing 0.02814815
Clothing trade-Textiles trade 0.02101010
Forestry-Textiles trade 0.01743590
Textiles dyeing-Textiles trade 0.03012346
We see that the index by Howard et al. (2016) is structured differently than the indicators presented above: Although they are based on exactly the same data, the value for forestry and clothing trade (XCL ≈ 0.019) is not equal to the value for clothing trade and forestry (XCL ≈ 0.024). Why? The XCLab is the difference between the colocation index, CLab, and the mean of a set of bootstrap samples, CLabRND (see Table 6). These random samples are drawn again each time a XCL value is computed, consequently, also the XCL value changes.
5 Proximity and accessibility
5.1 Distance-based measures of accessibility and proximity using individual point-level data
In this chapter, we mix two different concepts of indicators, accessibility and spatial proximity (see Table 10), both frequently used especially in the context of GIS (geographic information systems). Both concepts are discussed together because they have two aspects in common: 1) they are based on the geographical distance between point locations, in particular, the distance between an origin point i or several origin points (i = 1,...,n) and one or more destination points j (j = 1,...,m), and 2) for the calculation, they require geocoded (with geographical coordinates) individual point data.
| Indicator | Non-normalized | Normalized
| |
| Accessibility/Market potential | |||
| Harris | Mj = ∑ i=1nOidij-1 | ||
| 0 ≤ Mj ≤∞ | |||
| Hansen | Ai = ∑ j=1mOjf(dij) | Ai* =
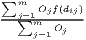 | |
| i≠j | i≠j
| ||
| 0 ≤ Ai ≤∞ | 0 ≤ Ai*≤ 1
| ||
| where: f(dij) = dij-λ or f(dij) = e-λ*dij
| |||
| or f(dij) =
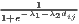 | |||
| Proximity | |||
| Count within buffer | Ni = ∑ i=1nI(dij ≤ t) | ||
| i≠j | |||
| Weighted count within buffer | Niw = ∑ i=1nI(dij ≤ t)Oj | ||
| i≠j | |||
| Ripley | Kt = 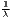 ∑
i=1n ∑
i=1n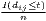 | Lt = 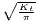 | Ht = Lt - t |
| i≠j | i≠j | i≠j | |
| E(Kt) = πt2 | E(Lt) = t | E(Ht) = 0 | |
where: λ = 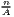 | |||
Notes: dij is the distance from origin location i (i = 1,...,n) to destination location j (j = 1,...,m), Oj is a variable quantifying the size of destination j, t is a maximum search radius and I(dij ≤ t) is the indicator function taking the value of I = 1 if dij ≤ t, and I = 0 otherwise.
Compiled from: Kiskowski et al. (2009); Krider, Putler (2013); Peña Carrera (2002); Pooler (1987); Reggiani et al. (2011); Smith (2016)
One popular indicator of accessibility is the Hansen accessibility, developed by Hansen (1959) in the context of land use theory. The basic idea is that “accessibility” equals the sum of opportunities outgoing from a specific origin i. These opportunities are spread over a set of m locations (j = 1,...,m). The summation is weighted with the distance between i and the j-th location. This distance, no matter how measured (e.g. street distance, Euclidean distance, driving time) is assumed to be perceived in a nonlinear way, which is operationalized by a nonlinear distance decay function (a.k.a. distance impedance function or response function), e.g. power, exponential or logistic. A similar concept was introduced by Harris (1954) attempting to model the market potential of locations. If we replace the inverse distance weighting in the Harris indicator with another type of distance weighting, we see that both concepts are mathematically equivalent. The only difference is that the Harris indicator is conceptualized from the supplier’s perspective j (e.g. market potential of a retail store) and the Hansen accessibility takes the demand location i as a starting point (Pooler, 1987; Reggiani et al., 2011). As these indicators are dimensionless and range from zero to infinity, a normalization with a range from zero to one can be computed by weighting the results with the opportunities without distance correction.
This accessibility/potential concept can be used in the regional economic context e.g. to quantify the over-regional job potential (e.g. Wieland, Fuchs 2018) or the clustering of point locations of a specific type, such as retail stores (e.g. Larsson, Öner 2014). The most common application of these indicators may be the context of transport economics and transport geography (e.g. Albacete et al. 2017).
In the GIS context, spatial proximity can be measured using concentric zones within a radius of t (buffers) around point i, where the number of the j points within this radius is counted (Longley et al., 2005). A systematic analysis of spatial proximity or cluster patterns is possible using Ripley’s K function (Ripley, 1976). It compares empirical point counts with expected values from a random spatial point process based on a Poisson distribution. Ripley’s K computes empirical values for each distance band with a maximum distance of t, which can be compared to the expected value. A more comprehensible (and linear) interpretation is provided when normalizing the K function in the form of the L or H function. Also, confidence intervals for the expected values can be calculated by bootstrapping (Kiskowski et al., 2009; Smith, 2016). All of these measures are based on a simple indicator function, I(dij ≤ t), which takes the value of I = 1 if point j is within a distance of t from point i or not (I = 0). Originating from natural sciences, especially Ripley’s K is frequently used when analyzing location patterns in spatial economic contexts, such as the clustering of retail stores (e.g. Krider, Putler 2013) or other types of firms assumed to be connected in a network (e.g. Espa et al. 2010).
5.2 Application in REAT
5.2.1 REAT functions for accessibility and proximity on the point level
Table 11 shows the REAT functions for the accessibility and proximity methods described above. A simple Euclidean distance matrix for georeferenced points (data frame with latitude and longitude) can be calculated using the function dist.mat(). The function dist.buf() computes a “count points within buffer”, where also a weighting, Oj, can be summarized (e.g., if the destination points are cities of a given population, one could count the number of cities within 50 kilometers and their corresponding population). The latter function uses dist.mat(), thus, it is not necessary to create a distance matrix before.
| Indicator | REAT function | Mandatory arguments | Optional arguments | Output |
| Distance | dist.mat() | data frame(s) with start | i≠j | data frame with |
| matrix | points i (ID, lat, lon) and | from, to, from-to | ||
| end points j (ID, lat, lon), | and distance dij | |||
| distance unit | (distance matrix) | |||
| Buffer | dist.buf() | data frame(s) with start | i≠j, sum Oj | list with distance |
| points (ID, lat, lon) and | at endpoints | matrix (data frame) | ||
| end points (ID, lat, lon), | and count table | |||
| max. distance t, | (data frame) | |||
| distance unit | ||||
| Hansen/ | hansen() | distance matrix (data | distance constant, | data frame with |
| Harris | frame with start points i | max. distance t, | origins i and | |
| and end points j as well | i≠j | accessibility Ai | ||
| as distance dij and Oj), | ||||
| weighting functions, | ||||
| parameters λ and γ | ||||
| Ripley | ripley() | data frame with points | local K values, | visible: matrix with t, Kt, |
| (ID, lat, lon), total area | confidence | E(Kt), Kt - E(Kt), Lt | ||
| A, max. distance t, | intervals | and Ht for each distance | ||
| number of distance | no. of samples, | interval, invisible: matrix | ||
| intervals | significance level, | (as described above) | ||
| plot (K, L or H) | and optional: matrices | |||
| with local K values and | ||||
| confidence intervals | ||||
Source: own compilation.
The same is the case for the function ripley(), which calculates Ripley’s K function for georeferenced data (data frame with lat/lon) and a given number of distance intervals up to a maximum distance of t. The differences between the empirical values, Kt, and the expected values, E(Kt), as well as the normalizations (Lt and Ht) are calculated and returned automatically. Optionally, local K values for each distance interval and corresponding confidence intervals are computed. These confidence intervals are based on bootstrapping with a given number of samples (default: 100) on a given significance level (the default value is α = 0.05, which leads to confidence intervals of a range from α∕2 = 2.5% to 1 - α∕2 = 97.5%). Note that the plot of the K function (or, when desired, L or H function) provides a graphical and more intuitive interpretation of the analyzed point pattern, especially when including confidence intervals.
When calculating the Hansen accessibility (or the Harris market potential) with hansen(), a distance matrix including the opportunities, Oj, is required. This can be, of course, done with dist.mat() (if straight-line distances are sufficient), but also with any other software creating distance matrices (and any type of transport costs indicator). In hansen(), the user may choose between a power, exponential or logistic distance decay function. Optionally, the normalized Hansen accessibility is returned additionally.
5.2.2 Application example 1: Location analysis of medical practices
In the example in Section 2.2.2, we dealt with small-scale regional inequality in health care in South Lower Saxony, Germany. We have seen that e.g. psychotherapists are more spatially clustered than general practitioners (GPs). Returning to this topic, we want to use proximity and accessibility measures for determining the market potential (in the sense of the Harris model) of these health care locations. Obviously, there are different location patterns of general practitioners and psychotherapists. In the related study, there was evidence that psychotherapists are not just clustered but clustered within some districts of larger cities (Wieland, Dittrich, 2016). In the German health care planning system, the market potential of medical practices is the main determinant of the official authorization to be included into the allocation system of health insurance, while psychotherapists are assumed to need quite larger market areas than GPs (Kassenärztliche Bundesvereinigung, 2013). Consequently, our research hypothesis is that the population potential of psychotherapists is larger than that of general practitioners.
We use the same test data as in the mentioned example, containing the health locations (GoettingenHealth1) and the corresponding settlements (GoettingenHealth2). We load both R datasets:
data(GoettingenHealth2)
Table GoettingenHealth1 contains 617 locations, whose ID is stored in the column location. Columns lat and lon contain the latitude and longitude, respectively, while the corresponding location type can be found in column type (phys_gen: general practitioners, psych: psychotherapists, pharm: pharmacies). As the following applications may be time-consuming, we extract the general practitioners from GoettingenHealth1 and draw a random sample of ten doctor’s practices:
# general practitioners: column "type" is equal to "phys_gen"
physgen_sample <- physgen[sample(nrow(physgen),10),]
# random sampling of ten general practitioners
Now, we want to summarize the population potential of these health locations in a 1,000 meters buffer. We apply the function dist.buf() to the sample data physgen_sample and sum up the local population of the districts within this distance (column pop in GoettingenHealth2):
GoettingenHealth2, "district", "lat", "lon", bufdist = 1000,
ep_sum = "pop")
# counting all districts within a radius of 1000 meters
# and summing the corresponding population
We calculate the arithmetic mean of all ten potentials:
[1] 8027.7
On average, the ten GP practices have a population potential of about 8,028 inhabitants. One problem related to the buffer technique is the lack of distance weighting: All origin points up to a given distance are included completely, while all points above 1,000 meters are ignored. Thus, we repeat estimating the population potential using the Hansen accessibility. At first, we need an origin-destination matrix (distance matrix) from the origin points to the sampled GP locations. We use the function dist.mat() and merge the returned distance matrix with the population values from GoettingenHealth2:
physgen_sample, "location", "lat", "lon")
# creating OD matrix from all districts to the
# sampled general practitioners
physgen_od <- merge (physgen_od, GoettingenHealth2,
by.x = "from", by.y = "district")
# merging with GoettingenHealth2 to include the
# population values of the districts
Then, we use the function hansen() to calculate the Hansen accessibility (used in the sense of the Harris market potential model) for each GP location in physgen_od.
The required columns in this dataset are the IDs of the GP locations (to), the IDs of the districts (from) and the population of the districts (pop) as well as the distances calculated above (distance). Finally, we have to set a distance weighting (which has an important influence in all types of spatial interaction models like this). For this purpose, we fall back on the results of a study by Fülöp et al. (2011): Based on empirical patient’s choice of doctor, they estimated distance decay functions in spatial interaction models (Huff model) for several types of physicians. For GPs, an exponential distance decay function with λ = -0.28 was found to fit the empirical data best. To set a distance decay function type and the related weighting(s), the function arguments dtype and lambda must be used. We save the results under the name physgen_hansen:
"distance", dtype = "exp", lambda = -0.28)
# calculating Hansen accessibility for the ten
# sampled general practitioners
The output of the hansen() function is:
J = 420 locations with mean attractivity = 1138.486
I = 10 origins with mean transport costs = 28.07581
Attractivity weighting (pow) with Gamma = 1
Distance weighting (exp) with Lambda = -0.28
to accessibility
1 1103 24267.054
2 1171 17629.564
3 1206 9581.732
4 1220 9213.407
5 197 10023.854
6 301 6489.571
7 600 69676.232
8 755 66921.123
9 966 13154.921
10 974 3666.171
Again, we calculate the arithmetic mean of the distance-weighted market potentials:
[1] 23062.36
The average population potential of the ten GPs is equal to 23,063 inhabitants.
As we want to compare the market potential of GPs and psychotherapists, we repeat the same analysis for them, now in the “fast mode”, leaving out most comments, as the functions and commands are exactly the same as above, only applied to psychotherapists.
psych_sample <- psychgen[sample(nrow(psychgen),10),]
psych_pot <- dist.buf (psych_sample, "location", "lat", "lon",
GoettingenHealth2, "district", "lat", "lon", bufdist = 1000,
ep_sum = "pop")
mean2(psych_pot$count_table$sum_pop)
[1] 12245.88
The calculation of Hansen accessibility is different from the one for GPs with respect to the assumed distance reaction of the (potential) clients: For psychotherapists, Fülöp et al. (2011) found a distance impedance which is considerably smaller than for GPs (and any other type of doctor), resulting in a weighting parameter of λ = -0.11 in the exponential decay function:
psych_sample, "location", "lat", "lon")
psych_od <- merge (psych_od, GoettingenHealth2,
by.x = "from", by.y = "district")
psych_hansen <- hansen (psych_od, "to", "from", "pop",
"distance", dtype = "exp", lambda = -0.11)
Hansen Accessibility
J = 420 locations with mean attractivity = 1138.486
I = 10 origins with mean transport costs = 25.56756
Attractivity weighting (pow) with Gamma = 1
Distance weighting (exp) with Lambda = -0.11
to accessibility
1 1031 43415.63
2 1213 39226.26
3 179 33491.41
4 313 51228.41
5 506 147887.43
6 786 147969.39
7 791 147971.80
8 811 148021.51
9 872 147475.57
10 922 42424.51
mean2(psych_hansen$accessibility)
[1] 94911.19
We see that the average population potential of the sampled psychotherapists on the 1,000 meters buffer level is equal to 12,246 inhabitants, which is about one third more than for GPs. The Hansen/Harris market potential of psychotherapists of about 94,911 persons is a fourfold increase compared to the GPs. We have to remember that the last result is not only a matter of location but also due to a lower assumed distance decay. However, the population potential of the sampled psychotherapists is obviously higher than the potential of the GPs, which can be attributed to a different location pattern, where psychotherapists are more clustered within larger city districts.
5.2.3 Application example 2: Clustering of health service providers
We stick to the example of health care locations. As we have found different degrees of regional inequality with respect to suppliers (Section 2.2.2) and of market potentials (Section 5.2.2), we now analyze the clustering patterns of health service providers. In South Lower Saxony there is nearly the same number of psychotherapists (118) and pharmacies (120), but we should not expect their location patterns to be similar or even equal. Following the results above, we hypothesize that psychotherapists are more spatially clustered than pharmacies (as we already know about clustering with respect to districts in the former case and we can expect an avoidance tendency in the latter case due to a high degree of substitutability).
For this analysis, we compute Ripley’s K with the REAT function ripley(). Before going on, we have to prepare two things: First, we load the required dataset. Then, we must calculate the total area of the study area manually (here: in square meters).
area_goe <- 1753000000
# area of Landkreis Goettingen (sqm)
area_nom <- 1267000000
# area of Landkreis Northeim (sqm)
area_gn <- area_goe+area_nom
Now, we compute Ripley’s K for the pharmacies only, which means processing only those locations in GoettingenHealth1 which are pharmacies (type == "pharm"). We set our maximum search radius equal to t = 30000 (function argument t.max), divided into 300 distance intervals (t.sep), resulting in distance steps of 100 meters. As we want to check for a significant deviation from a random spatial pattern, we instruct the function to construct confidence intervals (ci.boot = TRUE) using the default settings (α = 0.05, 100 bootstrapping samples). We also plot the results (default function argument: K.plot = TRUE) to inspect our results graphically. Here, we plot Kt, which is also the default setting (if the user wants to plot Lt or Ht instead, the function argument Kplot.func has to be changed to “L” or “H”, respectively):
"location", "lat", "lon", area = area_gn, t.max = 30000, t.sep = 300,
K.local = TRUE, ci.boot = TRUE, ci.alpha = 0.05, ciboot.samples = 100,
plot.title = "Ripley’s K: Clustering of pharmacies")
The output is a matrix with six columns and one row for each distance interval. Thus, we skip the full output here:
n = 120 points
t <= K t exp K t Kt-Kt exp L t H t
1 100 31415.93 3355556 3324140 1033.492 933.49238
2 200 125663.71 12583333 12457670 2001.349 1801.34940
3 300 282743.34 25586111 25303368 2853.824 2553.82412
4 400 502654.82 32297222 31794567 3206.326 2806.32580
5 500 785398.16 39008333 38222935 3523.739 3023.73923
...
We repeat the computation of Ripley’s K for the psychotherapists:
"location", "lat", "lon", area = area_gn, t.max = 30000, t.sep = 300,
K.local = TRUE, ci.boot = TRUE, ci.alpha = 0.05, ciboot.samples = 100,
plot.title = "Ripley’s K: Clustering of psychotherapists")
The output is (also truncated):
n = 118 points
t <= K t exp K t Kt-Kt exp L t H t
1 100 31415.93 30798621 30767205.2 3131.055 3031.055025
2 200 125663.71 48583740 48458076.6 3932.516 3732.516350
3 300 282743.34 80249928 79967184.8 5054.141 4754.141421
4 400 502654.82 132737719 132235064.2 6500.133 6100.132940
5 500 785398.16 202143062 201357664.2 8021.480 7521.479612
...
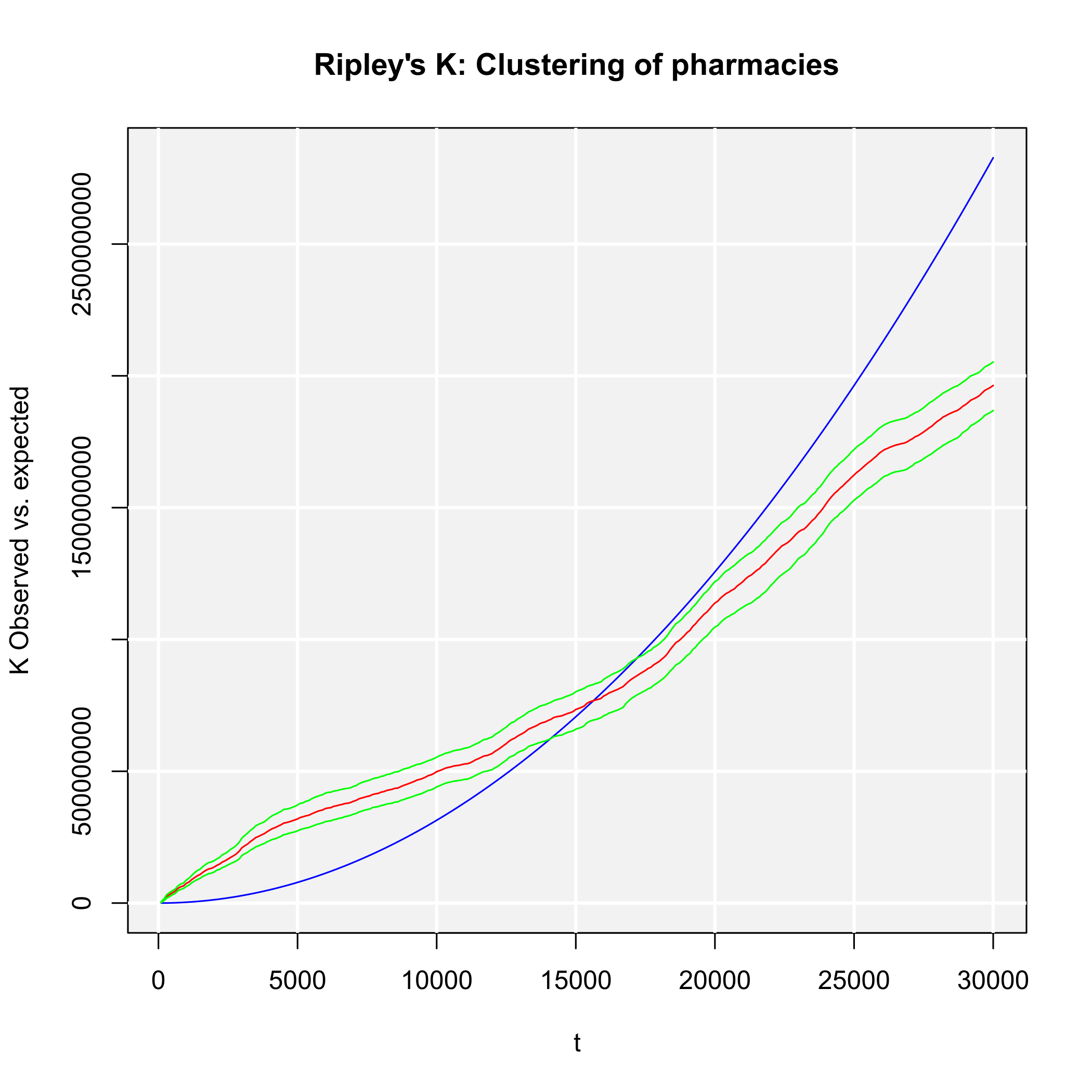 (a) Pharmacies (n=120)
(a) Pharmacies (n=120)  (b) Psychotherapists (n=118)
(b) Psychotherapists (n=118)
The graphical output is shown in Figures 4a (pharmacies) and 4b (psychotherapists), respectively. The expected value of Kt is plotted as blue line, while the empirical Kt values are red and the corresponding confidence intervals are colored in green (These colors are the default values in ripley() and can be changed by the function arguments lcol.exp and lcol.emp, respectively). As we have nearly the same number of points in both cases within the same field area, a direct comparison seems reasonable. Obviously, both types of locations show a significant spatial clustering: Also the pharmacies are more clustered than expected on condition of complete spatial randomness up to a distance of about 15,000 meters. We have to remember that also the population is already clustered (see Section 2.2.2) and the spatial distribution of pharmacies may follow this pattern. However, the clustering of psychotherapists exceeds this level enormously, especially within smaller distances up to about 8,000 meters. In conclusion, the psychotherapists are more spatially clustered than pharmacies.
6 Analysis and prognosis of regional growth
6.1 Tools and models concerning regional growth
6.1.1 Analyzing regional growth: shift-share analysis and portfolio matrix
Aspects of regional growth have already been discussed in the context of regional convergence in Section 3. The identification of clusters was the topic of Section 4. Combining some aspects of both, this section presents a collection of tools and models concerning regional growth with respect to industries. Like the indicators in Section 4, these techniques are of high significance especially in the context of local economic policy and municipal business promotion activities, aiming at e.g. strengthening a city’s or region’s competitiveness, defining its profile or increasing the number of jobs (Dinc, 2015; Nischwitz et al., 2017). Inspired by Farhauer, Kröll (2014) and congruent with the mathematical formulations in Section 4, we calculate on the basis of local/regional employment, eij, which is the number of employees of industry i in region j. Its growth from time t to time t + y can be operationalized as an absolute value (Δeij = eijt+y -eijt) or as a relative growth (Δeijrg = eijt+y∕eijt) or as a (percentage) growth rate (Δeijgr = eijt+y∕eijt - 1).
The first technique described is the regional economic portfolio matrix, originating from the portfolio matrix in marketing, developed by the Boston Consulting Group (BCG) for the identification of growing and declining business fields of firms (Henderson, 1973). However, this technique can also be applied to several regional economic contexts (Baker et al., 2002; Howard, 2007). Here, we present a portfolio matrix which compares the growth in one region with the growth in a superordinate reference region (e.g. whole economy). When using the matrix in this way, it is a plot of the growth rate with respect to industry i in the region (Δeijgr) on the x axis and the corresponding growth in the reference region (Δeigr) on the y axis (see Figure 5a). The size of the points for each industry may be the total size of employment in the region (eij) to reflect the absolute relevance of the i-th industry. The plot is segmented into four quadrants, differentiated with respect to positive or negative growth rates. As implied by the colors of the quadrants, they can be interpreted as follows: Quadrant I (top right) contains the industries growing in both the region and the whole economy (or any other reference region). Quadrant II (top left) shows all industries growing in the whole economy but shrinking in the regarded region, which may indicate significant locational handicaps. Quadrant III (bottom left) includes all industries shrinking in the region as well as in the whole economy. Quadrant IV (bottom right) shows the special case of “star” industries, indicating that these industries grow in the regarded region while shrinking in the whole economy. Note that this segmentation (and the corresponding interpretation) differs from the original BCG matrix.
 (a) Regional growth portfolio
(a) Regional growth portfolio 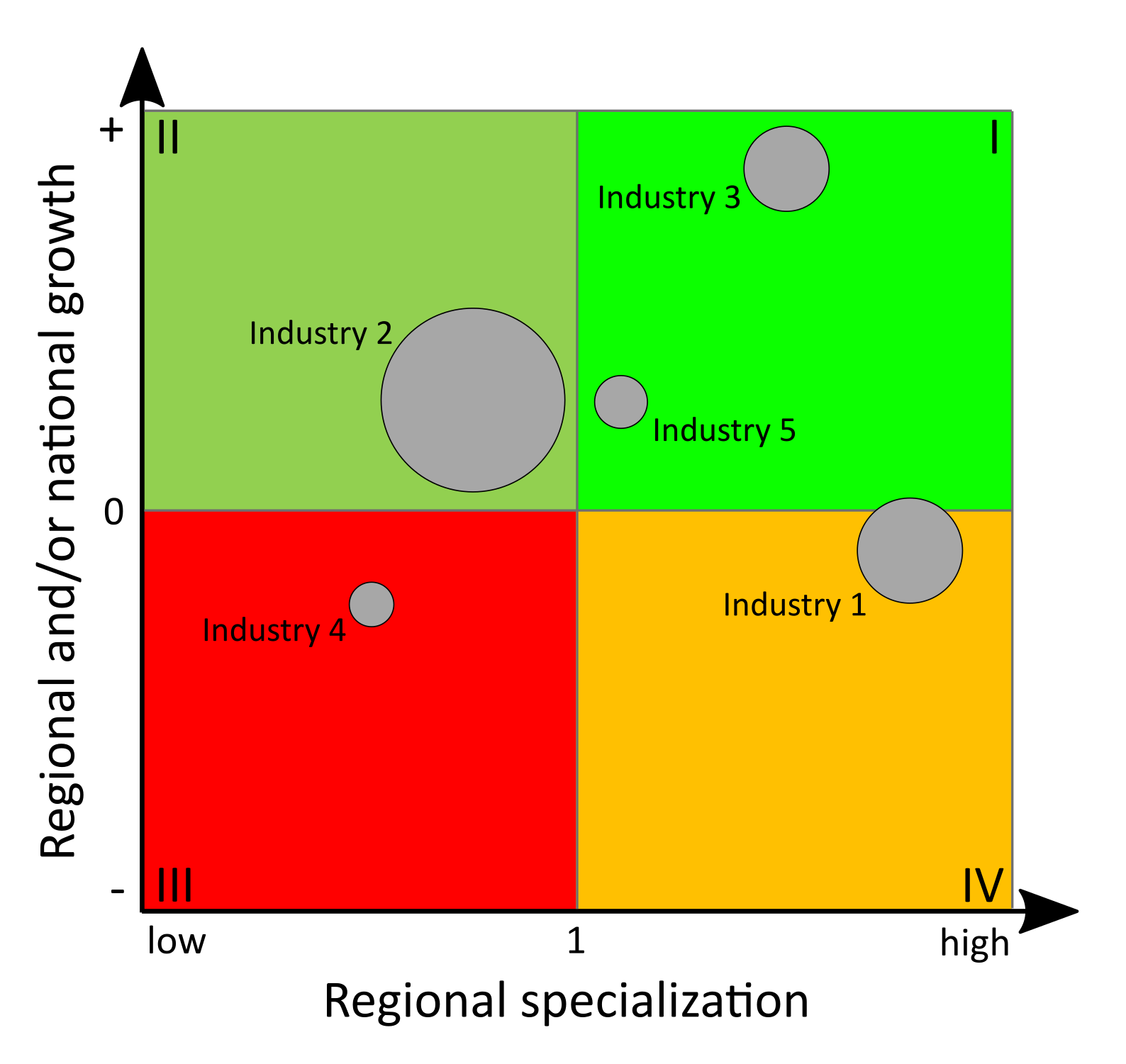 (b) Regional growth & specialization portfolio
(b) Regional growth & specialization portfolio
Another variant of the portfolio matrix, which was developed in the context of designing the REAT package, is shown in Figure 5b. Combining the aspects of regional specialization (see Section 4) and regional growth, we can plot the location quotient as an indicator of local specialization on the x axis, while plotting an industry-specific growth indicator on the y axis. For identifying “growing” industries, there are at least three options of operationalization: We can plot the industry-specific regional growth rate (Δeijgr) on the y axis (which is on the x axis in the portfolio matrix in Figure 5a) or the industry-specific national rate (Δeigr) or, if we want to show regional growth in relation to national growth, the quotient of industry-specific regional and national growth rates (Δeijgr∕Δeigr). In quadrant I, we see now all industries overrepresented in the region (in terms of the location quotient) as well as growing on the regional/national level. Quadrant II shows all industries underrepresented in the region but growing as well. In quadrants III and IV, we can identify all industries with negative growth rates, which are underrepresented or overrepresented, respectively.
| Component | Dunn-type (absolute) | Gerfin-type (index) |
| Δej = ejt+y - ejt = | ||
| njt,t+y + mjt,t+y + cjt,t+y | ||
| Net total shift | tt+y = ejt+y - ejt - njt,t+y = | tt+y = mjt,t+ycjt,t+y = 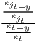 |
| mjt,t+y + cjt,t+y | ||
static (two time periods t and t + y)
| ||
| National share | njt,t+y = ejt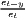 - ejt - ejt | njt,t+y = 1 (omitted) |
| Industrial mix | mjt,t+y = ∑
i=1Ieij
t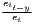 - ejt - ejt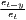 | mjt,t+y = 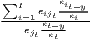 |
| Regional share | cjt,t+y = ∑
i=1Ieij
t(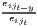 - -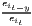 ) ) | cjt,t+y =  |
dynamic (T time periods, while T > 2)
| ||
| National share | njt,T = ∑
t=1Tej
t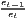 - ejt - ejt |
|
| Industrial mix | mjt,T = ∑
t=1T∑i=1Ieij
t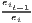 - ejt - ejt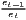 |
|
| Regional share | cjt,T = ∑
t=1T∑i=1Ieij
t(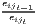 - -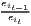 ) ) |
|
industry-specific
| ||
| National share | njt,t+yi = eijt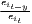 - eijt - eijt |
|
| Regional share | cjt,Ti = eijt(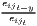 - -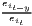 ) ) |
|
prognosis for time period z
| ||
| Employment | Δeijt+z = eijt+y(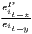 )cjt,t+y )cjt,t+y |
|
Notes: ejt is the employment in region j at time t, eijt is the employment of industry i in region j at time t, et is the total employment in the whole economy at time t, eit is the total employment in industry i, y and z are numbers of time periods added to t (z > y), T is the number of regarded time periods and I is the number of industries.
Compiled from: Farhauer, Kröll (2014); Haynes, Parajuli (2014); Schätzl (2000); Schönebeck (1996); Spiekermann, Wegener (2008); Barff, Knight (1988)
A well-established model of regional growth is the shift-share analysis, which is, although developed independently from the portfolio matrix, closely linked to the concept presented above. The original shift-share analysis was introduced by Dunn Jr. (1960) and given a theoretical foundation by Casler (1989). Parallelly and independently, Gerfin (1964) developed a variant of shift-share analysis, which is more popular in the German-speaking regional economic science. Both concepts have been extended in several ways. Table 12 shows the basics of shift-share analysis with respect to “Dunn” and “Gerfin” type. As there are several ways of formulating the shift-share formulae and calling the particular elements of the shift-share analysis, the description here is based on the mathematical formulations in Farhauer, Kröll (2014) and the terms used in Haynes, Parajuli (2014).
The basic idea of shift-share analysis is the decomposition of regional growth into components, recognizing that single economic regions are embedded into and influenced by a larger regional system, normally the whole economy, just called “the nation” hereinafter: The (employment or e.g. gross value added) growth of industry i in region j from time t to time t + y can be attributed to 1) a national trend, which means the economic climate in the whole system of regions, 2) the all-over growth or decline of the regarded industries and 3) the industry-specific performance of the region, which is linked to locational advantages or disadvantages. The first component is called national share and reflects the growth in region j that would have occurred if region j would have developed exactly as the nation. The second component is the industrial mix, representing the aggregated industry-specific growth in region j if the regarded industries would have developed like in the whole economy, adjusted by the national effect. The third component is the regional share, which is the “residuum” of the first two components; this share of growth is attributed to locational advantages (or disadvantages), showing the regional growth adjusted by national and industry effects (Farhauer, Kröll, 2014; Haynes, Parajuli, 2014).
The Dunn-type models deal with absolute growth (Δeij or Δej), which is the sum of all shift-share components, and a net total shift, which is the sum of the industrial mix and the regional share (as these components are region-specific). Thus, this technique is also called the “difference method”. The Gerfin-type approaches express growth in terms of indices, while the net total shift for region j is the result of a multiplication of the industrial mix index and the regional share index, resulting in the alternative denomination “index method” (Schätzl, 2000).
Several extensions have been developed for the Dunn-type shift-share analysis (Haynes, Parajuli, 2014). One regular application calculates a shift-share analysis for each industry i in region j (instead of computing components for the whole region), while skipping the industrial mix effect. A main contribution was the dynamic shift-share analysis by Barff, Knight (1988). It extended the Dunn model by dealing with growth within a longitudinal cut of T years. Other extensions of the Dunn-type technique provide a deeper differentiation of the three components, which are regarded as correlated (e.g. Arcelus 1984; Esteban-Marquillas 1972).
6.1.2 Commercial area prognosis
Also developed independently in the context of German urban planning, a commercial area prognosis deals with an absolute (assumed) employment growth (Δeij) over T years, which is used to forecast the required commercial area within a city or region j up to time T. Note that “commercial area” represents the type of urban area which is used by specific economic activities, especially industrial plants, and/or designated for this purpose in municipal land-use plans. This technique is a demand-side approach, as it derives the required commercial area from the (expected) demand for it (Bonny, Kahnert, 2005). See Table 13 for the calculation of two types of commercial area prognosis based on employment growth.
| Prognosis | GIFPRO | TBS-GIFPRO |
| Employment | eijtA =   eijt0 eijt0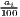 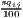  + +  eijt0 eijt0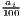 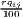  ![]](267157x.png) | eijtA =   eijt eijt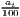   + +  eijt eijt   ![]](267167x.png) |
- eijt0 eijt0  | - eijt eijt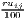  |
|
| where: eijt = f(t) = a + bt or | ||
| f(t) = atb or f(t) = aebt or | ||
f(t) =  |
||
| Areal index | pre-defined: aiij | empirical estimation: aiij =  |
| Commercial area | Aijt = eijtAaiij
| |
| Ajt = ∑
i=1IAij
t
| ||
| AjT = ∑
i=1I∑t=1TAij
t
| ||
Notes: eijtA is the (expected) number of employees of industry i in region j which is located in commercial areas at time t, eijt0 is the employment of industry i in region j at start time t0 (empirical value), eijt is the (expected) employment of industry i in region j at time t, ai is the share of employees in industry i which is located in commercial areas, sqij is the resettlement rate with respect to industry i in region j in one time period, rqij is the relocation rate with respect to industry i in region j in one time period, ruij is the reutilization rate with respect to industry i in region j in one time period, aiij is the areal index with respect to industry i in region j (commercial area per employee), Aijt is the (expected) commercial area for industry i in region j at time t, Ajt is the (expected) commercial area in region j at time t and AjT is the sum of the (expected) commercial area in region j over all T time periods.
Compiled from: Bonny, Kahnert (2005); CIMA Projekt + Entwicklung GmbH et al. (2011); Deutsches Institut für Urbanistik GmbH, Spath + Nagel (GbR) (2010); Planungsgruppe MWM (2009); Mulligan (2006); Vallée et al. (2012)
The basic model called GIFPRO (German abbreviation for “Gewerbe- und Industrieflächenbedarfsprognose”, roughly translated: prognosis of future demand of commercial area) was developed by Stark et al. (1981). The usual procedure is to estimate – starting from the current employment – the future industry-specific employment in region j. This number of employees is weighted by the industry-specific shares of workers usually located in commercial areas and multiplied by a resettlement rate (sqij percent of employees from industry i are resettled in one time period) and a relocation rate (rqij percent of employees from industry i are relocated in one time period) as well as a reutilization rate (ruij percent of employees from industry i will be located at reused commercial area). This “commercial area-relevant” employment is weighted with an areal index, aij (commercial area per employee), to compute the commercial area for industry i in region j for one time period t. The expected commercial area is summed over all I industries (Ajt) and, finally, over all T years and I industries (AjT) (Bonny, Kahnert, 2005; Planungsgruppe MWM, 2009).
A significant extension was developed in the context of establishing a land-use plan for Dresden: The TBS-GIFPRO (German abbreviation for “Trendbasierte und standortspezifische Gewerbe- und Industrieflächenbedarfsprognose”, roughly translated: trend-based and location-specific prognosis of future demand of commercial area) technique (Deutsches Institut für Urbanistik GmbH, Spath + Nagel (GbR), 2010). It includes a stochastic approach for forecasting employment as well as other region-specific data. The employment prognosis is done using a trend regression model (employment against time) based on past empirical employment data for region j (mostly from official employment statistics) which are used for forecasting future employment. For each i industry, a single regression model is estimated, where the function type is not pre-defined but chosen e.g. based on the explained variance (R2) and/or plausibility considerations.
The function may be linear (which seems unrealistic) or not: Deutsches Institut für Urbanistik GmbH, Spath + Nagel (GbR) (2010) use linear and exponential functions. However, from the growth perspective, also a logistic function may be applied (see Mulligan 2006 for a discussion of logistic growth with respect to population). If possible, the areal index and, maybe, other parameters are also estimated empirically for the specific region j (e.g. via firm-level surveys and/or official statistical data).
6.2 Application in REAT
6.2.1 REAT functions for analyzing and forecasting regional growth
Table 14 shows the functions for the analysis of regional growth as implemented in REAT. Table 15 presents the functions related to commercial area prognosis. All of these functions require at least current employment data for each industry in the regarded region j, eij, which may be a single numeric vector or the column of a data frame or matrix. Another similarity of all mentioned functions is the optional argument of the industry names (or codes). If no industry names are stated by the user (default function argument: industry.names = NULL), the industries are numbered consecutively. With respect to the function output, all regional growth functions distinguish between a visible and an invisible output (see e.g. Section 3), where the main results are returned automatically and the details are included in the invisible output (mostly a list with several entries of type matrix).
| Model | REAT function | Mandatory arguments | Optional arguments | Output |
| Growth | portfolio() | vectors of eijt and eijt+y | point size | visible: plot, |
| portfolio | and vectors of eit and | factor, | invisible: growth | |
| matrix | eit+y or matrix/data | industry names | rates (matrix) | |
| frame with eijt and | ||||
| eit for T years, | ||||
| point size (e.g. eijt+y) | ||||
| Growth and | locq.growth() | vectors of eijt and eijt+y | point size | visible: plot, |
| specialization | and vectors of eit and | factor, | invisible: list with | |
| portfolio | eit+y or matrix/data | industry names | portfolio data | |
| matrix | frame with eijt and | (matrix), LQij | ||
| eit for T years, | (matrix) and | |||
| point size (e.g. eijt+y) | growth rates | |||
| (matrix) | ||||
| Shift-share | shift() | vectors of eijt and eijt+y, | shift-share | visible: matrix |
| analysis | vectors of eit and eit+y | method | with components, | |
| (default: Dunn), | invisible: list with | |||
| industry names, | components (matrix), | |||
| plot components, | growth (matrix) and | |||
| plot portfolio | shift method (char), | |||
| optional: plot(s) | ||||
| dynamic | shiftd() | vectors of eijt0 and eit0, | shift-share | visible: matrix |
| matrix/data frame with | method | with annual | ||
| eijt and eit for T years | (default: Dunn), | components, | ||
| industry names, | invisible: list with | |||
| plot components, | components (matrix), | |||
| plot portfolio | annual components | |||
| (matrix), growth | ||||
| (matrix) and shift | ||||
| method (char), | ||||
| optional: plot(s) | ||||
| industry- | shifti() | vectors of eijt and eijt+y, | shift-share | visible: matrix |
| specific | vectors of eit and eit+y | method | with industry | |
| (default: Dunn), | components, | |||
| industry names, | invisible: list with | |||
| plot components, | components (matrix), | |||
| plot portfolio | industry components | |||
| (matrix), growth | ||||
| (matrix) and shift | ||||
| method (char), | ||||
| optional: plot(s) | ||||
| industry- | shiftid() | vectors of eijt0 and eit0, | shift-share | visible: matrix |
| specific and | matrix/data frame with | method | with industry | |
| dynamic | eijt and eit for T years | (default: Dunn), | components, | |
| industry names, | invisible: list with | |||
| plot components, | components (matrix), | |||
| plot portfolio | industry components | |||
| (matrix), growth | ||||
| (matrix) and shift | ||||
| method (char), | ||||
| optional: plot(s) | ||||
| prognosis | shiftp() | vectors of eijt and eijt+y, | industry names, | visible: matrix |
| vectors of eit and eit+y, | plot | with industry | ||
| vector of eit+zP | components, | |||
| invisible: list with | ||||
| industry employment | ||||
| prognosis (matrix), | ||||
| components (matrix), | ||||
| industry components | ||||
| (matrix), growth | ||||
| (matrix) and shift | ||||
| method (char), | ||||
| optional: plots | ||||
Source: own compilation.
| Model | REAT function | Mandatory arguments | Optional arguments | Output |
| GIFPRO | gifpro() | vectors of eij, ai, | vector of ruij, | visible: total |
| sqij, rqij and aiij, | industry names, | commercial area and | ||
| time interval, | type of output | (optional) annual values, | ||
| time base | invisible: list with | |||
| components (matrices), | ||||
| annual and all-over | ||||
| results (list with two | ||||
| matrices) | ||||
| TBS-GIFPRO | gifpro.tbs() | vectors of eijt for T | vector of ruij, | visible: total |
| years, ai, sqij, rqij | industry names, | commercial area and | ||
| and aiij, time interval, | type of output, | (optional) annual values, | ||
| time base, trend | employment | invisible: list with | ||
| function types | forecast only | components (matrices), | ||
| annual and all-over | ||||
| results (list with two | ||||
| matrices), industry- | ||||
| specific forecast | ||||
| model results (list | ||||
| with I matrices) | ||||
Source: own compilation.
The portfolio matrix (growth portfolio and growth-specialization portfolio, respectively) can be plotted using the functions portfolio() and locq.growth(), respectively. The different techniques of shift-share analysis are distributed over five functions (shift(), shiftd(), shifti(), shiftid() and shiftp()). The usage of portfolio and shift-share functions is similar: In any case, the user needs industry-specific employment data for the regarded region and the reference region (e.g. whole economy) for at least two time periods (e.g. years).
All functions for shift-share analysis (except for shift-share prognosis with shiftp()) provide three variants of calculation of the components: The classical Dunn method (default function argument shift.method="Dunn"), the Dunn extension by Esteban-Marquillas (1972) (shift.method="Esteban") producing four components instead of three, and the Gerfin method (shift.method="Gerfin"). When calculating a dynamic shift-share analysis, the user must choose the function shiftd(). Industry-specific components are returned by the function shifti(). With shiftid() one can combine both approaches. Here, it is important to recognize that the function structure allows a combination of e.g. industry-specific and dynamic components while calculating the components from the Esteban-Marquillas extension of shift-share analysis. Additionally, the shift-share functions may plot a portfolio matrix (function argument plot.portfolio = TRUE), allowing portfolio and shift-share analysis at once.
Both functions for commercial area prognosis (gifpro() and gifpro.tbs()) require vectors of employment data as well as the coefficients for resettlement etc. When forecasting commercial area using the trend-specific technique with gifpro.tbs(), the user needs time series data of previous industry-specific employment and has to specify a trend function type (linear, power, exponential or logistic) for each industry. The “best” function type may be examined visually by regarding the employment forecasting output (optional function argument prog.plot = TRUE) and the related R2 values which is part of the invisible function output. Note that this function uses the REAT function curvefit(), which is a simple tool for bivariate regression, similar to the curve fitting functions in other spreadsheet or statistics software.
6.2.2 Application example 1: Analysis of regional growth in Göttingen
Referring to the example in Section 4.2.2, we perform a regional growth analysis for the German city Göttingen. We use the same dataset Goettingen as before, that contains industry-specific employment data for Göttingen and Germany from 2008 to 2017. We load our example data:
In the first step, we want to examine the industry-specific growth in Göttingen visually. Using the function portfolio(), we plot a regional growth matrix with respect to the 15 industries (rows 2 to 16). We also set a plot title (argument pmtitle) and axis labels (arguments pmx and pmy, respectively) as well as industry-specific colors (argument pcol):
Goettingen$Goettingen2017[2:16],
Goettingen$BRD2008[2:16], Goettingen$BRD2017[2:16],
psize = Goettingen$Goettingen2017[2:16], psize.factor = 15,
pmtitle = "Growth of 15 industries in Göttingen",
industry.names = Goettingen$WZ2008_Code[2:16],
pmx = "Growth Göttingen 2008-2017 [%]",
pmy = "Growth Germany 2008-2017 [%]",
pcol.border = "grey",
pcol = c("darkgreen", "powderblue", "chocolate", "darkred",
"orange", "cadetblue1", "chartreuse1", "red", "coral",
"coral4", "cyan", "darkcyan", "yellow", "green", "deeppink"),
leg = TRUE, leg.x = -90)
Similarly, we plot a growth-specialization portfolio matrix using locq.growth() with the same options (colors etc.). On the y axis, we put the industry-specific regional growth which is stated by the function argument y.axis = "r" (if we would like to see the national growth instead, we had to set y.axis = "n"; for the quotient of regional and national growth, use y.axis = "rn"):
Goettingen$Goettingen2017[2:16],
Goettingen$BRD2008[2:16], Goettingen$BRD2017[2:16],
psize = Goettingen$Goettingen2017[2:16], psize.factor = 15,
y.axis = "r", industry.names = Goettingen$WZ2008_Code[2:16],
pmtitle = "Growth and specialization in Göttingen",
pmx = "Regional specialization Göttingen",
pmy = "Growth Göttingen 2008-2017 [%]", pcol.border = "grey",
pcol = c("darkgreen", "powderblue", "chocolate", "darkred",
"orange", "cadetblue1", "chartreuse1", "red", "coral",
"coral4", "cyan", "darkcyan", "yellow", "green", "deeppink"),
leg = TRUE, leg.x = 0.1)
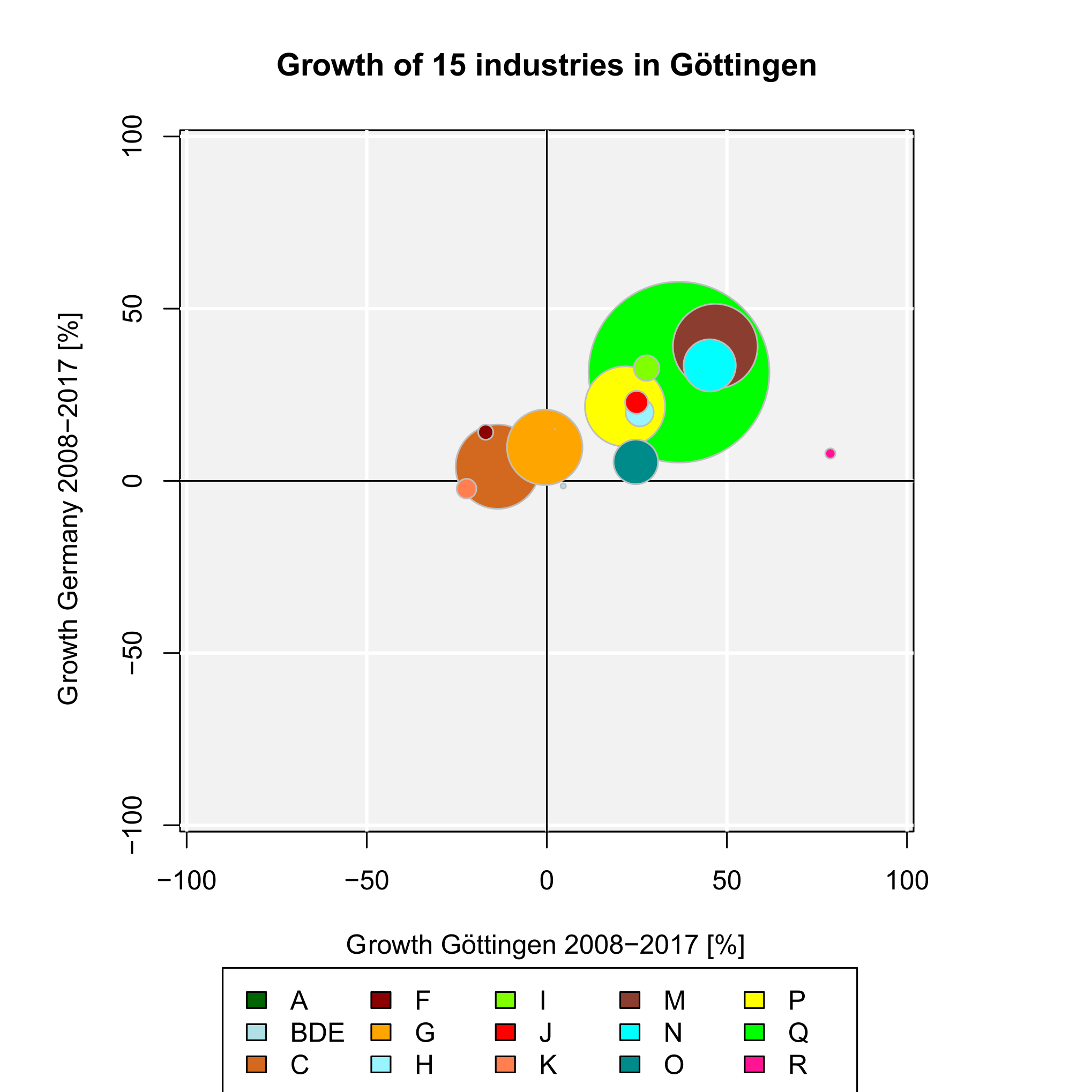 (a) Growth portfolio matrix for Göttingen
(a) Growth portfolio matrix for Göttingen
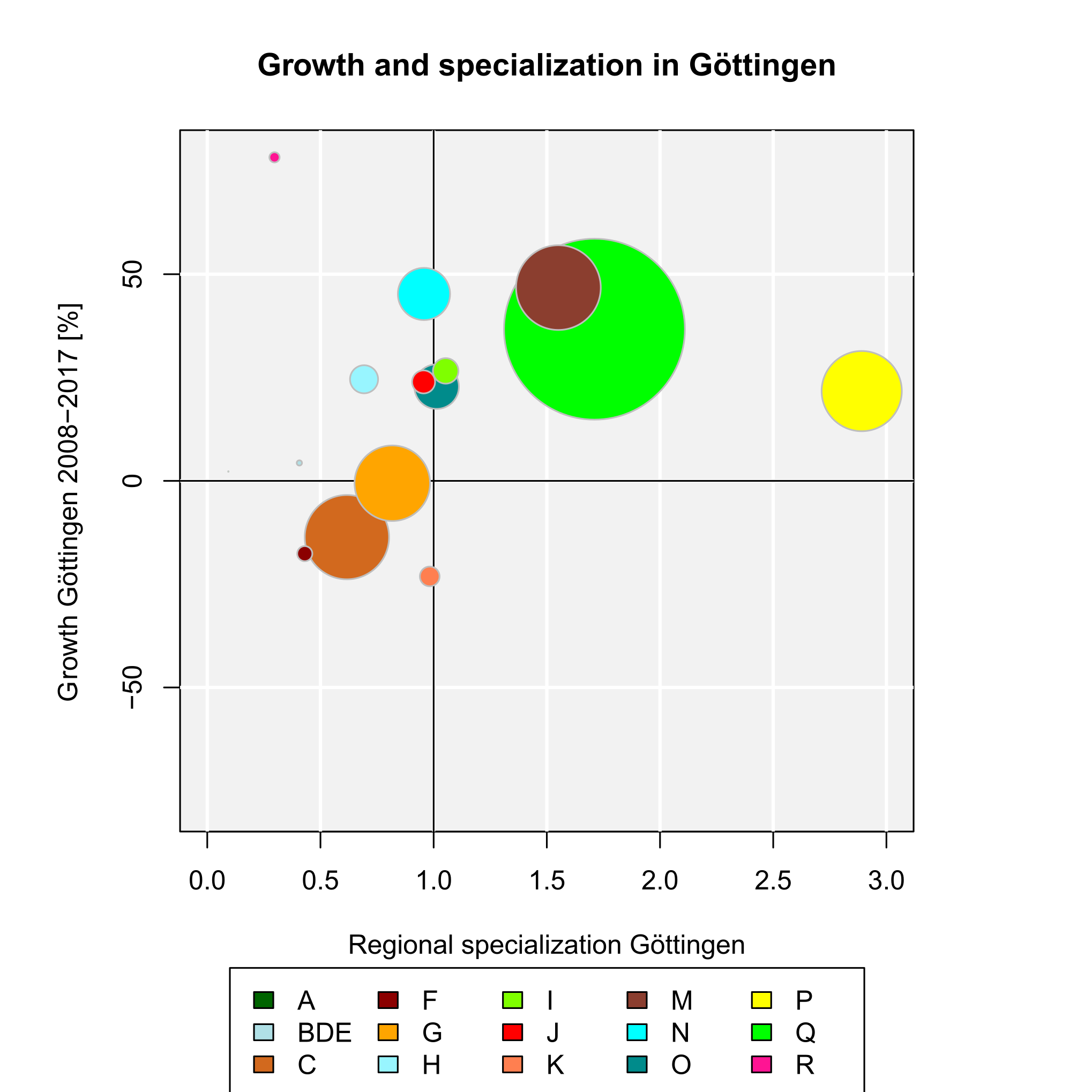 (b) Growth-specialization matrix for Göttingen
(b) Growth-specialization matrix for Göttingen
The resulting growth portfolio matrix is shown in Figure 6a, the growth-specialization portfolio in Figure 6b. The size of the points (or bubbles) is equal to the current industry-specific employment (eij) for 2017 (rows 2 to 16 of column Goettingen2017 in the example data), normalized with respect to a maximum point size of 15 (argument psize.factor = 15). As we can see, the health sector (industry code Q, green bubble) has the highest absolute relevance, which can be attributed to the local university hospital (see Section 4.2.2). The axes in the growth portfolio are segmented at x = 0 and y = 0, respectively, which means a differentiation between positive and negative growth. As we can see, most industries have grown from 2008 to 2017 in both the region and the whole economy (see quadrant I) with similar growth rates. There is one outlier: Industry R (arts, entertainment, and recreation) shows a regional growth of more than 75 percent, while the national growth is about 10 percent. Note that we see percentage growth rates from 2008 to 2017 here (if average growth rates are desired, use the function argument time.periods).
Looking at the growth-specialization portfolio, we can identify absolute relevance and growth rate as well as regional specialization of the industries (The colors and bubble sizes are equal to those in Figure 6a). In quadrant I, we find the industries which are overrepresented in Göttingen (specialization) and growing at this regional level. As expected in this university city and related to our results in Section 4.2.2, the “stars” in Göttingen are education (code P), health (code Q) and professional, scientific and technical services (code M).
While the portfolio matrix analysis tells us about the industry-specific growth, the shift-share analysis decomposes this growth into the national, industrial and regional components. In the first step, we perform a static shift-share analysis in the sense of Dunn Jr. (1960) for the same data as in the portfolio analysis by applying the function shift():
Goettingen$BRD2008[2:16], Goettingen$BRD2017[2:16])
# rows 2-6: 15 industries
# columns Goettingen2008 and Goettingen2017:
# employment Goettingen 2008 and 2017, respectively
# columns BRD2008 and BRD2017:
# employment Germany 2008 and 2017, respectively
This is our (visible) output:
Method: Dunn
Shift-share components
Components
Growth (t1-t) 10411.0000
National share 9178.1916
Industrial mix 2204.8202
Regional share -972.0118
Net total shift 1232.8084
Calculation for 15 industries
Regional employment at time t: 56872, at time t+1:
67283 (10411 / 18.30602 %)
National employment at time t: 27695398, at time t+1:
32164973 (4469575 / 16.13833 %)
In this cross-sectional analysis, we see that the overall employment in Göttingen increased by 10,411 persons from 2008 to 2017. However, a large share of this growth is due to the growth in the national economy (njt,t+y ≈ 9,178 employees), which is only a bit lower than Göttingen. The industrial mix component (mjt,t+y) shows that approximately 2,205 additional employees must be attributed to an overrepresentation of growing industries in Göttingen. The regional share is negative (cjt,t+y ≈-972), which indicates locational disadvantages. When interpreting the industrial mix also as a regional aspect (which seems plausible), we can look at the sum of the industrial mix and the regional share: The net total shift (tt+y) is equal to 1,233 employees, representing the growth difference between the region and the whole economy.
We confirm our results using the Gerfin technique. We request it by setting the argument shift.method of the shift() function equal to "Gerfin":
Goettingen$BRD2008[2:16], Goettingen$BRD2017[2:16],
shift.method = "Gerfin")
The output is:
Method: Gerfin
Shift-share components
Components
Industrial mix 1.0333810
Regional share 0.9857591
Net total shift 1.0186647
Calculation for 15 industries
Regional employment at time t: 56872, at time t+1:
67283 (10411 / 18.30602 %)
National employment at time t: 27695398, at time t+1:
32164973 (4469575 / 16.13833 %)
In the index method, there is no national share component (implicitly, it is equal to one), thus, we only take a look at the industrial mix and the regional share as well as the net total shift. The industrial mix component is above one (njt,t+y ≈ 1.03), showing a more advantageous sector structure in Göttingen compared to Germany. While the regional share in the Dunn-type shift-share analysis was negative, this component in the Gerfin analysis is slightly below one (cjt,t+y ≈ 0.99), indicating locational disadvantages.
These traditional techniques only regard the overall growth with respect to cross-sectional data. To gain a deeper insight and take into account also seasonal effects, we perform a dynamic shift-share analysis in the sense of Barff, Knight (1988) which distinguishes between the 15 industries simultaneously. This can be done via the REAT function shiftid(), requiring data for the initial time period and at least for two following periods. In the Goettingen dataset, the rows 2 to 16 represent the industries and the columns represent the years (2008 to 2017). Data for the regarded region and the whole economy is arranged successively. We also use the industry codes in column WZ2008_Code. In this function, we have to define the start and end periods explicitly:
Goettingen$BRD2008[2:16], Goettingen[2:16,13:22],
time1 = 2008, time2 = 2017,
industry.names = Goettingen$WZ2008_Code[2:16])
# columns 3-12: employment in Göttingen 2009-2017
# columns 13-22: employment in Germany 2009-2017
The result is:
Method: Dunn
Shift-share components
A BDE C F G
Growth (t1-t) -3.000000 29.00000 -1117.0000 -255.0000 -51.0000
National share 6.103502 -9.46377 254.5217 160.0638 561.7436
Regional share -9.103502 38.46377 -1371.5217 -415.0638 -612.7436
Net total shift -9.103502 38.46377 -1371.5217 -415.0638 -612.7436
H I J K M
Growth (t1-t) 524.0000 470.00000 274.00000 -465.000000 2229.000
National share 368.2053 515.03493 286.32383 6.356612 1821.392
Regional share 155.7947 -45.03493 -12.32383 -471.356612 407.608
Net total shift 155.7947 -45.03493 -12.32383 -471.356612 407.608
N O P Q R
Growth (t1-t) 1178.0000 268.0000 1272.0000 4211.000 363.00000
National share 977.9869 167.9118 1138.5383 3556.692 47.50353
Regional share 200.0131 100.0882 133.4617 654.308 315.49647
Net total shift 200.0131 100.0882 133.4617 654.308 315.49647
Calculation for 15 industries
Regional employment at time t: 56872, at time t+1:
67283 (10411 / 18.30602 %)
National employment at time t: 27695398, at time t+1:
32164973 (4469575 / 16.13833 %)
The visible output is a matrix containing one row for each component (the number of components depends on the selected shift-share method, here: Dunn) and I columns (one for each industry). As we calculate industry-specific components, there is no industrial mix effect, which means that the calculations are on the level of single industries. Again, we detect large absolute growth for industries P (education) and Q (health) (see Table 9). Interestingly, this growth can be mainly attributed to effects in the whole economy. The corresponding regional shares are small but positive, showing locational advantages with respect to these industries in Göttingen.
The logic of shift-share analysis can also be regarded in two other examples: If industry C (manufacturing) had developed as in the national trend, the absolute growth in Göttingen would be equal to 255 employees. In fact, there was a decline of 1,117 employees, resulting in a negative regional share of -1,372 employees, indicating locational disadvantages with respect to the manufacturing sector. The opposite is true for the industries with code BDE (including electricity, gas, water supply, etc.): The absolute growth of 29 employees would not have occurred if this sector had developed as in the whole economy (negative national share equal to -9 employees). The residuum (regional share) is equal to 38 employees, indicating a trend contrary to the national.
6.2.3 Application example 2: Commercial area prognosis for Göttingen
Using the same data, we now perform a commercial area prognosis for Göttingen. We load our data:
When using the GIFPRO-based commercial area prognosis techniques, several parameters have to be defined (employment shares in commercial areas ai, resettlement rate sqij, relocation rate rqij and areal index aiij; a reutilization rate ruij is optional, thus, we ignore the reutilization of commercial area in this example). These parameters have to be defined for each industry. In our example, we use the employment shares as well as the resettlement and relocation rates from Deutsches Institut für Urbanistik GmbH, Spath + Nagel (GbR) (2010). Note that some sectors are, per definition, not located within commercial areas (e.g. agriculture), resulting in an employment share of ai = 0. As we want to reuse the sets of parameters, we save them as single numeric vectors:
# industry-specific shares of employees in commercial areas
sq_quote <- c(0.77, 0.77, 0.15, 0.15, 0.77, 0.15, 0.77, 0.77,
0.77, 0.77, 0.77, 0.77, 0.77, 0.77, 0.77)
# industry-specific resettlement quote
rq_quote <- rep(0.7, 15)
# industry-specific relocation quote (0.7 for each of the 15 industries)
area_index <- c(0, 0, 200, 75, 250, 250, 50, 100, 100, 100, 100,
50, 50, 50, 50)
# industry-specific area index (sqm commercial area per employee)
Now, we compute the traditional commercial area prognosis using the gifpro() function and the Goettingen data as well as the parameters defined above. We forecast the commercial area for five years (tinterval = 5). Our base is 2017 (time.base = 2017), as this is the last year empirical data is available for. We save the (invisible) output in the list object gifpro_goettingen:
a_i = ca_share, sq_ij = sq_quote, rq_ij = rq_quote, tinterval = 5,
ai_ij = area_index, time.base = 2017,
industry.names = Goettingen$WZ2008_Code[2:16], output = "full")
As we have set output = "full", the visible function output contains overall as well as annual values:
Method: GIFPRO
Employment and commercial area changes (allover)
Employment Commercial Area
Sum 1113.8785 212981.94
Average 222.7757 42596.39
Employment and commercial area changes (per time unit)
Employment CommercialArea
2018 222.7757 42596.39
2019 222.7757 42596.39
2020 222.7757 42596.39
2021 222.7757 42596.39
2022 222.7757 42596.39
Calculation for 15 industries
In all 15 industries, 1,114 new employees are predicted for the year 2022, resulting in 212,928 square meters required for new commercial area. As the employment prognosis is not based on (nonlinear) trend regression but on constant growth, the absolute employment growth and the required commercial area are equal in each year (223 employees and 42,596 sqm, respectively).
The object gifpro_goettingen contains a list called components containing the single components of prognosis as well as the results already shown in the visible output (results). To understand the GIFPRO technique and the related REAT function, we take a look at the single components:
$resettlement
2018 2019 2020 2021 2022
A 0.00000 0.00000 0.00000 0.00000 0.00000
BDE 0.00000 0.00000 0.00000 0.00000 0.00000
C 11.81100 11.81100 11.81100 11.81100 11.81100
F 1.80090 1.80090 1.80090 1.80090 1.80090
G 38.00489 38.00489 38.00489 38.00489 38.00489
H 3.72150 3.72150 3.72150 3.72150 3.72150
I 1.73327 1.73327 1.73327 1.73327 1.73327
J 3.12928 3.12928 3.12928 3.12928 3.12928
K 2.67806 2.67806 2.67806 2.67806 2.67806
M 12.18910 12.18910 12.18910 12.18910 12.18910
N 7.50750 7.50750 7.50750 7.50750 7.50750
O 0.00000 0.00000 0.00000 0.00000 0.00000
P 0.00000 0.00000 0.00000 0.00000 0.00000
Q 0.00000 0.00000 0.00000 0.00000 0.00000
R 0.00000 0.00000 0.00000 0.00000 0.00000
$relocation
2018 2019 2020 2021 2022
A 0.0000 0.0000 0.0000 0.0000 0.0000
BDE 0.0000 0.0000 0.0000 0.0000 0.0000
C 55.1180 55.1180 55.1180 55.1180 55.1180
F 8.4042 8.4042 8.4042 8.4042 8.4042
G 34.5499 34.5499 34.5499 34.5499 34.5499
H 17.3670 17.3670 17.3670 17.3670 17.3670
I 1.5757 1.5757 1.5757 1.5757 1.5757
J 2.8448 2.8448 2.8448 2.8448 2.8448
K 2.4346 2.4346 2.4346 2.4346 2.4346
M 11.0810 11.0810 11.0810 11.0810 11.0810
N 6.8250 6.8250 6.8250 6.8250 6.8250
O 0.0000 0.0000 0.0000 0.0000 0.0000
P 0.0000 0.0000 0.0000 0.0000 0.0000
Q 0.0000 0.0000 0.0000 0.0000 0.0000
R 0.0000 0.0000 0.0000 0.0000 0.0000
$reuse
2018 2019 2020 2021 2022
A 0 0 0 0 0
BDE 0 0 0 0 0
C 0 0 0 0 0
F 0 0 0 0 0
G 0 0 0 0 0
H 0 0 0 0 0
I 0 0 0 0 0
J 0 0 0 0 0
K 0 0 0 0 0
M 0 0 0 0 0
N 0 0 0 0 0
O 0 0 0 0 0
P 0 0 0 0 0
Q 0 0 0 0 0
R 0 0 0 0 0
$employment
2018 2019 2020 2021 2022
A 0.00000 0.00000 0.00000 0.00000 0.00000
BDE 0.00000 0.00000 0.00000 0.00000 0.00000
C 66.92900 66.92900 66.92900 66.92900 66.92900
F 10.20510 10.20510 10.20510 10.20510 10.20510
G 72.55479 72.55479 72.55479 72.55479 72.55479
H 21.08850 21.08850 21.08850 21.08850 21.08850
I 3.30897 3.30897 3.30897 3.30897 3.30897
J 5.97408 5.97408 5.97408 5.97408 5.97408
K 5.11266 5.11266 5.11266 5.11266 5.11266
M 23.27010 23.27010 23.27010 23.27010 23.27010
N 14.33250 14.33250 14.33250 14.33250 14.33250
O 0.00000 0.00000 0.00000 0.00000 0.00000
P 0.00000 0.00000 0.00000 0.00000 0.00000
Q 0.00000 0.00000 0.00000 0.00000 0.00000
R 0.00000 0.00000 0.00000 0.00000 0.00000
As we defined some industries as not relevant for commercial areas (ai = 0), they do not contribute any employees neither resettled nor relocated (such as A - agriculture, B - mining and quarrying or R - arts, entertainment, and recreation). We see that e.g. in the manufacturing sector (code C), there is an annual increase of about 12 employees attributed to resettlement and 55 employees related to relocation each year (see row 3 in resettlement and relocation, respectively). As we ignored the reutilization of commercial area, the matrix containing the commercial area-relevant employment related to reutilization (reuse) contains only zeros. The sum of all three components is stored in the fourth matrix, employment. There is an annual increase of nearly 67 employees in the manufacturing sector. The contents of the results list is the same as shown in the visible output.
In the next step, we apply the trend-based commercial area prognosis (TBS-GIFPRO) to the Goettingen data. In the gifpro.tbs() function, we use the employment data from 2008 to 2017 (columns 3 to 12), and assume an exponential function for employment prognosis (function argument prog.func, repeating the argument "exp" for each industry). The employment prognosis is plotted (prog.plot = TRUE), showing all 15 plots in one (plot.single = FALSE):
a_i = ca_share, sq_ij = sq_quote, rq_ij = rq_quote, tinterval = 5,
prog.func = rep("exp", nrow(Goettingen[2:16,3:12])),
ai_ij = area_index, time.base = 2008,
industry.names = Goettingen$WZ2008_Code[2:16],
prog.plot = TRUE, plot.single = FALSE, output = "full")
The visible function output is similar to the output above:
Method: TBS-GIFPRO
Employment and commercial area changes (allover)
Employment CommercialArea
Sum 1139.6592 216012.46
Average 227.9318 43202.49
Employment and commercial area changes (per time unit)
Employment CommercialArea
2018 224.9565 42945.53
2019 226.2904 43054.76
2020 227.7755 43182.97
2021 229.4169 43330.70
2022 231.2199 43498.50
Calculation for 10 industries
The resulting plot containing the employment forecasting functions is shown in Figure 7. The black vertical lines divide the plots into the esimation segment (2008 to 2017) and the prognosis segment (2018 to 2022). Four function types are supplied: linear (blue), power (green), exponential (yellow) and logistic (red). Note that a linear trend seems unrealistic as it implies continuous growth and may result in negative employment if the slope is negative. At this point, we should normally discuss and find the “best” forecasting model for each industry and rerun our analysis a few times. In our example, we skip this step and just take a look at the prognosis functions: In most cases, an exponential growth (or decline) seems to be an appropriate approximation. The power functions (green lines) are nearly invisible as their data fit is nearly the same as that of the exponential functions. Thus, we could choose them instead. In our case, the exponential function seems sufficient.
As expected, a nonlinear industry growth results in a nonlinear overall employment growth and, consequently, the commercial area-relevant employment also grows in a nonlinear way. As we can see from the gifpro.tbs() output, employment increases by about 228 employees per year on average and by about 1,140 employees over the five years regarded (2018 to 2022). The annual commercial area required ranges from 42,946 sqm (2018) to 43,499 sqm (2022), all in all 216,012 sqm up to 2022. In our case, the estimated commercial area exceeds the prognosis derived from the simple GIFPRO analysis, which can be attributed to the positive differences between the exponential prognosis and a linear prognosis (see Figure 7). We skip the inspections of the components, which could be addressed by saving the results in an object (list), as we did in the first GIFPRO example.
7 Final remarks
This paper has shown how R and specifically the package REAT can be used for regional economic analysis. It should be noted that this package aims at width with respect to the treated analysis subjects rather than depth. The subsections provide the basic analysis methods regarded as most important from the package developer’s point of view (with respect to usage in current papers and discussion in current textbooks as well as application in own research projects), while there are several other approaches as well as extensions of the basic methods. A more detailed survey of the common methods can be found in the cited literature, especially in review articles (e.g. Nakamura, Morrison Paul 2009; Portnov, Felsenstein 2010) and textbooks (e.g. Farhauer, Kröll 2014).
Finally, we have to keep in mind that this package (like nearly any other free software) was developed in a non-commercial context (and published under the GNU General Public License). All functions have been tested several times using various real data and single functions have already been used in a few research projects. However, there is no warranty that all functions always work perfectly. Like nearly any other R package, REAT is continuously refined, which means extending functions as well as correcting errors. This requires attentive usage and, of course, constructive feedback from the package users. It can be easily transmitted using the contact information on the CRAN package website.
References
Albacete X, Olaru D, Paül V, Biermann S (2017) Measuring the accessibility of public transport: A critical comparison between methods in Helsinki. Applied Spatial Analysis and Policy 10[2]: 161–188. CrossRef.
Allington NF, McCombie J (2007) Economic Growth and Beta-Convergence in the East European Transition Economies. In: Arestis P, Baddeley M, McCombie J (eds), Economic Growth. Edward Elgar publishing, Cheltenham, 200–222
Arcelus FJ (1984) An extension of shift-share analysis. Growth and Change 15[1]: 3–8. CrossRef.
Bai CE, Tao Z, Tong YS (2008) Bureaucratic integration and regional specialization in China. China Economic Review 19[2]: 308–319. CrossRef.
Baker P, von Kirchbach F, Mimouni M, Pasteels JM (2002) Analytical Tools for Enhancing the Participation of Developing Countries in the Multilateral Trading System in the Context of the Doha Development Agenda. Aussenwirtschaft 57[3]: 343–372. https://EconPapers.repec.org/RePEc:usg:auswrt:2002:57:03:343-372
Balassa B (1965) Trade Liberalisation and “Revealed” Comparative Advantage. The Manchester School 33[2]: 99–123. CrossRef.
Barff RA, Knight PL (1988) Dynamic shift-share analysis. Growth and Change 19[2]: 1–10. CrossRef.
Barro RJ, Sala-i Martin X (2004) Economic Growth (2nd ed.). MIT Press
Bonny HW, Kahnert R (2005) Zur Ermittlung des Gewerbeflächenbedarfs. Raumforschung und Raumordnung 63[3]: 232–240
Capello R, Nijkamp P (2009) Introduction: Regional growth and development theories in the twenty-first century - recent theoretical advances and future challenges. In: Capello R, Nijkamp P (eds), Handbook of Regional Growth and Development Theories. 1–18
Casler SD (1989) A Theoretical Context for Shift and Share Analysis. Regional Studies 23[1]: 43–48. CrossRef.
Ceapraz IL (2008) The Concepts of Specialisation and Spatial Concentration and the Process of Economic Integration: Theoretical Relevance and Statistical Measures. The Case of Romania’s Regions. Romanian Journal of Regional Science 2[1]: 68–93
Charles-Coll JA (2011) Unterstanding Income Equality: Concept, Causes and Management. International Journal of Economics and Management Science 1[3]: 17–28
CIMA Projekt + Entwicklung GmbH, NIW Niedersächsisches Institut für Wirtschaftsforschung, NORD/LB Regionalwirtschaft, Planquadrat Dortmund GbR (2011) Gewerbeflächenkonzeption für die Metropolregion Hamburg (GEFEK). Research report
Cracau D, Durán Lima JE (2016) On the Normalized Herfindahl-Hirschman Index: A Technical Note. International Journal on Food System Dynamics 7[4]: 382–386
Damgaard C, Weiner J (2000) Describing inequality in plant size or fecundity. Ecology 81[4]: 1139–1142. CrossRef.
Dapena AD, Fernández Vázquez E, Rubiera Morollón F (2016) The role of spatial scale in regional convergence: the effect of MAUP in the estimation of β-convergence equations. The Annals of Regional Science 56[2]: 473–489. CrossRef.
Dauth W, Fuchs M, Otto A (2015) Standortmuster in Westdeutschland: Nur wenige Branchen sind räumlich stark konzentriert. IAB Kurzbericht 16/2015, Institut für Arbeitsmarkt- und Berufsforschung. http://doku.iab.de/kurzber/2015/kb1615.pdf
Dauth W, Fuchs M, Otto A (2018) Long-run processes of geographical concentration and dispersion: Evidence from Germany. Papers in Regional Science 97[3]: 569–593. CrossRef.
Deutsches Institut für Urbanistik GmbH, Spath + Nagel (GbR) (2010) Stadtentwicklungskonzept Gewerbe für die Landeshauptstadt Potsdam. Research report, Landeshauptstadt Potsdam. https://www.potsdam.de/sites/default/files/documents/STEK_Gewerbe_Langfassung_2010.pdf
Dinc M (2015) Introduction to Regional Economic Development. Major Theories and Basic Analytical Tools. Elgar
Dixon R, Freebairn J (2009) Trends in Regional Specialisation in Australia. Australasian Journal of Regional Studies 15[3]: 281–296
Doran J, Jordan D (2013) Decomposing European NUTS2 regional inequality from 1980 to 2009: National and European policy implications. Journal of Economic Studies 40[1]: 22–38. CrossRef.
Dunn Jr. ES (1960) A Statistical and Analytical Technique for Regional Analysis. Papers in Regional Science 6[1]: 97–112. CrossRef.
Duranton G, Puga D (2000) Diversity and Specialisation in Cities: Why, Where and When Does it Matter? Urban Studies 37[3]: 533–555. CrossRef.
Ellison G, Glaeser E (1997) Geographic Concentration in U.S. Manufacturing Industries: A Dartboard Approach. Journal of Political Economy 105[5]: 889–927
Espa G, Arbia G, Giuliani D (2010) Measuring industrial agglomeration with inhomogeneous K-function: the case of ICT firms in Milan (Italy). Department of Economics Working Papers 1014, Department of Economics, University of Trento, Italia
Esteban-Marquillas JM (1972) I. A reinterpretation of shift-share analysis. Regional and Urban Economics 2[3]: 249 – 255. CrossRef.
Farhauer O, Kröll A (2014) Standorttheorien. Regional- und Standortökonomik in Theorie und Praxis (2nd ed.). Springer, Heidelberg
Fujita M, Krugman P, Venables A (2001) The Spatial Economy: Cities, Regions, and International Trade (1st ed.), Volume 1. The MIT Press
Fülöp G, Kopetsch T, Schöpe P (2011) Catchment areas of medical practices and the role played by geographical distance in the patient’s choice of doctor. The Annals of Regional Science 46[3]: 691–706. CrossRef.
Furceri D (2005) Beta and sigma convergence: A mathematical relation of causality. Economics Letters 89[2]: 212–215. CrossRef.
Gerfin H (1964) Gesamtwirtschaftliches Wachstum und regionale Entwicklung. Kyklos 17[4]: 565–593. CrossRef.
Gini C (1912) Variabilità e Mutuabilità. Contributo allo Studio delle Distribuzioni e delle Relazioni Statistiche. Cuppini
Gluschenko K (2018) Measuring regional inequality: to weight or not to weight? Spatial Economic Analysis 13[1]: 36–59. CrossRef.
Goecke H, Hüther M (2016) Regional Convergence in Europe. Intereconomics 51[3]: 165–171. CrossRef.
Goschin Z, Constantin D, Roman M, Ileanu B (2009) Regional specialization and geographic concentration of industries in Romania. South-Eastern Europe Journal of Economics 1[1]: 99–113. https://ojs.lib.uom.gr/index.php/seeje/article/view/5536
Haas A, Südekum J (2005) Spezialisierung und Branchenkonzentration in Deutschland: Regionalanalyse. IAB-Kurzbericht 1/2005. http://hdl.handle.net/10419/158181
Habánik J, Hošták P, Kútik J (2013) Economic and social disparity development within regional development of the Slovak Republic. Economics and Management 18[3]: 457–464. CrossRef.
Hansen WG (1959) How Accessibility Shapes Land Use. Journal of the American Institute of Planners 25[2]: 73–76. CrossRef.
Harris CD (1954) The Market as a Factor in the Localization of Industry in the United States. Annals of the Association of American Geographers 44[4]: 315–348
Haynes KE, Parajuli J (2014) Shift-share analysis: decomposition of spatially integrated systems. In: Handbook of Research Methods and Applications in Spatially Integrated Social Science. Elgar, 315–344. CrossRef.
Heinemann M (2008) Messung und Darstellung von Ungleichheit. Working Paper Series in Economics 108, University of Lüneburg, Institute of Economics. https://EconPapers.repec.org/RePEc:lue:wpaper:108
Henderson BD (1973) The Experience Curve - Reviewed. IV. The Growth Share Matrix or The Product Portfolio. Reprint 135. https://www.bcg.com/documents/file13904.pdf
Herfindahl OC (1950) Concentration in the U.S. Steel Industry. Colombia University Press
Hirschman AO (1945) National Power and the Structure of Foreign Trade. Publications of the Bureau of Business and Economic Research. University of California Press
Hoen AR, Oosterhaven J (2006) On the measure of comparative advantage. The Annals of Regional Science 40[3]: 677–691. CrossRef.
Hoffmann J, Hirsch S, Simons J (2017) Identification of spatial agglomerations in the German food processing industry. Papers in Regional Science 96[1]: 139–162. CrossRef.
Hoover EM (1936) The Measurement of Industrial Localization. The Review of Economics and Statistics 18[4]: 162–171
Howard D (2007) A regional economic performance matrix – an aid to regional economic policy development. Journal of Economic and Social Policy 11[2]: article 4. https://EconPapers.repec.org/RePEc:usg:auswrt:2002:57:03:343-372
Howard E, Newman C, Tarp F (2016) Measuring industry coagglomeration and identifying the driving forces. Journal of Economic Geography 16[5]: 1055–1078
Huang Y, Leung Y (2009) Measuring Regional Inequality: A Comparison of Coefficient of Variation and Hoover Concentration Index. The Open Geography Journal 2[1]: 25–34. CrossRef.
Jiang L, Guan M, Tian J (2007) On Chinese Regional Specialization and Industry Concentration. In: 2007 International Conference on Machine Learning and Cybernetics, Volume 6, 3396–3400
Kabacoff RI (2017) Quick-R: Data Types. Manual. https://www.statmethods.net/input/datatypes.html
Kassenärztliche Bundesvereinigung (2013) Die neue Bedarfsplanung. Grundlagen, Instrumente und regionale Möglichkeiten. Brochure. https://www.kbv.de/media/sp/Instrumente_Bedarfsplanung_Broschuere.pdf
Kim S (1995) Expansion of Markets and the Geographic Distribution of Economic Activities: The Trends in U. S. Regional Manufacturing Structure, 1860–1987. The Quarterly Journal of Economics 110[4]: 881–908. CrossRef.
Kiskowski MA, Hancock JF, Kenworthy A (2009) On the Use of Ripley’s K-function and its Derivatives to Analyze Domain Skriderize. Biophysical Journal 97[4]: 1095–1103. CrossRef.
Kohn W, Öztürk R (2013) Statistik für Ökonomen. Datenanalyse mit R und SPSS (2nd ed.). Springer Gabler
Krider R, Putler DS (2013) Which Birds of a Feather Flock Together? Clustering and Avoidance Patterns of Similar Retail Outlets. Geographical Analysis 45[2]: 123–149. CrossRef.
Krugman P (1979) Increasing returns, monopolistic competition, and international trade. Journal of International Economics 9[4]: 469–479. CrossRef.
Krugman P (1991) Geography and trade. MIT Press
Larsson JP, Öner Ö (2014) Location and co-location in retail: a probabilistic approach using geo-coded data for metropolitan retail markets. The Annals of Regional Science 52[2]: 385–408. CrossRef.
Lehocký F, Rusnák J (2016) Regional specialization and geographic concentration: experiences from Slovak industry. Miscellanea Geographica – Regional Studies on Development 20[3]: 5–13. https://www.degruyter.com/downloadpdf/j/mgrsd.2016.20.issue-3/mgrsd-2016-0011/mgrsd-2016-0011.pdf
Lessmann C (2005) Regionale Disparitäten in Deutschland und ausgesuchten OECD-Staaten im Vergleich. ifo Dresden berichtet 3/2005: 25–33
Lessmann C (2014) Spatial inequality and development - Is there an inverted-U relationship? Journal of Development Economics 106: 35–51. CrossRef.
Lessmann C (2016) Regional inequality and internal conflict. German Economic Review 17[2]: 157–191. CrossRef.
Lessmann C, Seidel A (2017) Regional inequality, convergence, and its determinants – a view from outer space. European Economic Review 92: 110–132. CrossRef.
Litzenberger T, Sternberg R (2006) Der Clusterindex – eine Methodik zur Identifizierung regionaler Cluster am Beispiel deutscher Industriebranchen. Geographische Zeitschrift 94[2]: 209–224
Longley PA, Goodchild MF, Maguire DJ, Rhind DW (2005) Geographical Information Systems and Science (2nd ed.). Wiley
Lorenz MO (1905) Methods of measuring the concentration of wealth. Publications of the American Statistical Association 9[70]: 209–219. CrossRef.
Martin C (2015) Kreative Klasse 2015. Kreativität als entscheidender Faktor für wirtschaftlichen Erfolg: Entwicklungen und Ausprägungen in Deutschland. Research report. https://www.kreativ-sta.de/wp-content/uploads/2017/10/agiplan_Kreative_Klasse_2015_Studie.pdf
Midelfart-Knarvik K, Overman H, Redding S, Venables A (2000) The Location of European Industry. European Economy - Economic Papers 142
Moga LM, Constantin DL (2011) Specialization and Geographic Concentration of the Economic Activities in the Romanian Regions. Journal of Applied Quantitative Methods 6[2]: 12–21. https://pdfs.semanticscholar.org/aa9d/365d6a8ef4c3585595c8ba03fe373ab02010.pdf
Mulligan GF (2006) Logistic Population Growth in the World’s Largest Cities. Geographical Analysis 38[4]: 344–370. CrossRef.
Mussini M (2017) Decomposing Changes in Inequality and Welfare Between EU Regions: The Roles of Population Change, Re-Ranking and Income Growth. Social Indicators Research 130[2]: 455–478. CrossRef.
Myrdal G (1957) Economic theory and under-developed regions. G. Duckworth
Nakamura R, Morrison Paul C (2009) Measuring agglomeration. In: Capello R, Nijkamp P (eds), Handbook of Regional Growth and Development Theories. Elgar, 305–328
Nischwitz G, Böhme R, Fortmann F (2017) Kommunale Wirtschaftsförderung in Bremen: Handlungsrahmen, Programme und Wirkungen. Schriftenreihe Institut Arbeit und Wirtschaft 23/2017. http://hdl.handle.net/10419/172756
O’Donoghue D, Gleave B (2004) A Note on Methods for Measuring Industrial Agglomeration. Regional Studies 38[4]: 419–427. CrossRef.
OECD (2019) OECD Territorial Reviews. Website. https://www.oecd-ilibrary.org/fr/urban-rural-and-regional-development/oecd-territorial-reviews_19900759
Palan N (2017) Konzentrations- und Ungleichheitsindizes: ein methodischer Überblick sowie ein empirischer Vergleich anhand der Textilindustrie. Zeitschrift für Wirtschaftsgeographie 61[3-4]: 135–155. CrossRef.
Peña Carrera L (2002) Tracing accessibility over time: two swiss case studies. Technical report. http://hdl.handle.net/2099.1/6327
Petrakos G, Psycharis Y (2016) The spatial aspects of economic crisis in Greece. Cambridge Journal of Regions, Economy and Society 9[1]: 137–152. CrossRef.
Planungsgruppe MWM (2009) Flächennutzungsplanung Gemeinde Wachtberg - Fachbeitrag Arbeiten. Report. http://www.wachtberg.de/imperia/md/content/cms127/gemeindeentwicklung/fnp-fb-arbeiten-24-02-2009.pdf
Pooler J (1987) Measuring geographical accessibility: a review of current approaches and problems in the use of population potentials. Geoforum 18[3]: 269 – 289. CrossRef.
Porter ME (1990) The Competitive Advantage of Nations. Free Press
Portnov BA, Felsenstein D (2005) Measures of Regional Inequality for Small Countries. In: Felsenstein D, Portnov B (eds), Regional Disparities in Small Countries. 47–62. CrossRef.
Portnov BA, Felsenstein D (2010) On the suitability of income inequality measures for regional analysis: Some evidence from simulation analysis and bootstrapping tests. Socio-Economic Planning Sciences 44[4]: 212–219. CrossRef.
Puente S (2017) Regional convergence in Spain: 1980-2015. Research report. Economic Bulletin 3/2017, Banco de Espana
R Core Team (2018a) R: A Language and Environment for Statistical Computing. Software, Vienna, Austria. https://www.R-project.org/
R Core Team (2018b) The R Manuals. Manual. https://cran.r-project.org/manuals.html
Reggiani A, Bucci P, Russo G (2011) Accessibility and Impedance Forms: Empirical Applications to the German Commuting Network. International Regional Science Review 34[2]: 230–252. CrossRef.
Ricardo D (1821) On the Principles of Political Economy and Taxation (3rd ed.). McMaster University Archive for the History of Economic Thought
Ripley BD (1976) The second-order analysis of stationary point processes. Journal of Applied Probability 13[2]: 255–266. CrossRef.
RStudio Team (2016) RStudio: Integrated Development Environment for R. Software, RStudio, Inc., Boston, MA. http://www.rstudio.com/
Schmidt H (1997) Konvergenz wachsender Volkswirtschaften. Theoretische und empirische Konzepte sowie eine Analyse der Produktivitätsniveaus westdeutscher Regionen, Volume 152 of Wirtschaftswissenschaftliche Beiträge. Springer
Schönebeck C (1996) Wirtschaftsstruktur und Regionalentwicklung : theoretische und empirische Befunde für die Bundesrepublik Deutschland, Volume 75 of Dortmunder Beiträge zur Raumplanung Blaue Reihe. IRPUD
Schätzl L (2000) Wirtschaftsgeographie 2: Empirie (3rd ed.). Schöningh
Smith TE (2016) Notebook on Spatial Data Analysis. Technical report. http://www.seas.upenn.edu/~ese502/#notebook
Spiekermann K, Wegener M (2008) Modelle in der Raumplanung I: 4. Input-Output-Modelle. Presentation, Lecture “Modelle in der Raumplanung” WS 2008/2009. http://www.spiekermann-wegener.de/mir/pdf/MIR1_4_111108.pdf
Stark KD, Velsinger P, Bauer M, Bonny HW, Kricke J, Schwetlick D, Striedel HD (1981) Flächenbedarfsberechnung für Gewerbe- und Industrieansiedlungsbereiche: GIFPRO. Number 4.029 in Schriftenreihe Landes- und Stadtentwicklungsforschung des Landes Nordrhein-Westfalen. ILS, Dortmund
Statistisches Bundesamt (2008) German Classification of Economic Activities, Edition 2008. Dataset (XLS). https://www.destatis.de/DE/Methoden/Klassifikationen/GueterWirtschaftklassifikationen/klassifikationWZ08englisch.xls
Störmann W (2009) Regionalökonomik. Theorie und Praxis. Oldenbourg, Munich
Taylor JK, Cihon C (2004) Statistical Techniques for Data Analysis (2nd ed.). Taylor and Francis
Theil H (1967) Economics and information theory. North-Holland
Tian Z (2013) Measuring agglomeration using the standardized location quotient with a bootstrap method. Journal of Regional Analysis and Policy 43[2]: 186–197
Vallée D, Witte A, Brandt T, Bischof T (2012) Bedarfsberechnung für die Darstellung von Allgemeinen Siedlungsbereichen (ASB) und Gewerbe- und Industrieansiedlungsbereichen (GIB) in Regionalplänen. Research report, Staatskanzlei des Landes Nordrhein-Westfalen. https://www.wirtschaft.nrw/sites/default/files/asset/document/lep_nrw_flaechenbedarf_endbericht_endfassung_04122012.pdf
Vogiatzoglou K (2006) Increasing agglomeration or dispersion? Industrial specialization and geographic concentration in NAFTA. Journal of Economic Integration 21[2]: 379–396
von Neumann J, Kent RH, Bellinson HR, Hart BI (1941) The Mean Square Successive Difference. The Annals of Mathematical Statistics 12[2]: 153–162. CrossRef.
Weddige-Haaf K, Kool C (2017) Determinants of regional growth and convergence in Germany. Discussion paper. Discussion Paper Series 17-12, Utrecht University School of Economics
Wieland T (2019) REAT: Regional Economic Analysis Toolbox. R package version 3.0.1. Software. https://CRAN.R-project.org/package=REAT
Wieland T, Dittrich C (2016) Bestands- und Erreichbarkeitsanalyse regionaler Gesundheitseinrichtungen in der Gesundheitsregion Göttingen. Research report, Georg-August-Universität Göttingen, Geographisches Institut, Abteilung Humangeographie. http://webdoc.sub.gwdg.de/pub/mon/2016/3-wieland.pdf
Wieland T, Fuchs H (2018) Regionalökonomische Disparitäten im Spiegel von Raumtypisierungen. Ein Konzept zur Identifikation strukturell benachteiligter Gebiete in Südtirol (Italien). Standort - Zeitschrift für Angewandte Geographie 42[3]: 152–163. CrossRef.
Williamson JG (1965) Regional Inequality and the Process of National Development: A Description of the Patterns. Economic Development and Cultural Change 13[4]: 1–84
Yamamura S, Goto H (2018) Location patterns and determinants of knowledge-intensive industries in the Tokyo Metropolitan Area. Japan Architectural Review 1[4]: 443–456. CrossRef.
Young AT, Higgins MJ, Levy D (2008) Sigma Convergence versus Beta Convergence: Evidence from U.S. County-Level Data. Journal of Money, Credit and Banking 40[5]: 1083–1093. CrossRef.
 © 2019 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)
© 2019 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)