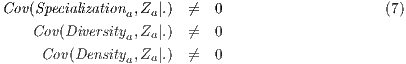Volume
6, Number 1, 2019, 17–24 journal homepage:
region.ersa.org
Volume
6, Number 1, 2019, 17–24 journal homepage:
region.ersa.orgDOI: 10.18335/region.v5i3.242
Agglomeration economies and urban productivity
1 Universidad Técnica Particular de Loja, Loja, Ecuador Received: 26 January 2018/Accepted: 21 November 2018Abstract. This study explores the relationship between agglomeration economies and industrial productivity between 1980 and 2010 in Ecuador. The measure of productivity used is labor productivity. We conclude that urbanization economies have a positive impact on productivity in the period analyzed. These results are consistent with other works for developed and developing countries.
JEL classification: R12
Key words: agglomeration, agglomeration economies, urban productivity, Ecuador
1 Introduction
The increasing concentration of people and production produces benefits known as economies of agglomeration in the economic literature. Traditionally, agglomeration economies are classified in location economies and urbanization economies.
From the seminal works of Glaeser et al. (1992) and Henderson et al. (1995), the ongoing debate is not only about the dichotomy between specialized and diversified environments within the same urban system, but also about the coexistence of specialization and diversity.
Following Glaeser et al. (1992), location economies or MAR1 externalities that operate within a specific industry restrict the flow of ideas to others, allowing the innovator to internalize externalities. Such interactions can positively influence the productivity of companies and the growth of cities. On the other hand, the urbanization of economies occurs through industries, which motivates the argument of Jacobs (1969) that the variety of industries within a geographical region promotes knowledge spillovers and results in innovative activities and economic growth. In this framework, the concepts of specialization and diversification are inherent to the economies of location and urbanization, respectively.
The empirical literature establishes that spatial concentration of industrial activity improves economic growth, productivity, and innovation through different approaches, among which the common denominator is the analysis of the location-urbanization dichotomy. In line with this literature, this study explores the relationship between the economies of agglomeration and industrial productivity between 1980 and 2010, years for which census data exist for the economic activity of the country. There are two motivations for this work. First, to contrast the economic literature and the empirical results broadly focused in developed countries with those of a developing country like Ecuador. Second, to contribute to the orientation and reform of economic policies related to the productivity of the country, which seeks to reorient its strong agro-export sector.
2 Industrial dynamism: Diversity of the cantons of Ecuador
The industrial sector is the second most important in terms of GDP in the Ecuadorian economy, but it is the most dynamic given that, unlike the other sectors, it has experienced 9% growth between 1980 and 2010 according to World Bank data. The services sector is the most relevant due to, among other things, the momentum generated in the eighties by exports and the oil boom that stimulated this sector, as well as that of the public administration. This is compounded by the significant growth in self-employed activities in the tertiary sector, whose participation in the national economically active population (EAP) in 1974 was 8.4%, 11.1% in 1982, and 28.5% in 2010. Finally, agriculture has fallen in its share of the national GDP by 6% in this period.
As in other countries, economic activity tends to agglomerate in relatively few cities: Guayaquil and Quito mainly, those that from colonization maintain their supremacy over the others, and therefore perform important economic, regional, and international functions. Although these cities have altogether only 3.29% of the total surface area, they contain 16.25% and 15.48% of the population, they generate 23.61% and 25.19% of the gross added value, and represent 21.35% and 28.91% of manufacturing employment, respectively. Based on the information available for Ecuador at the industry and canton level, Figure 1 shows the productivity growth in the analysis period for cantons whose increase is above the average annual growth rate of 4.2%.
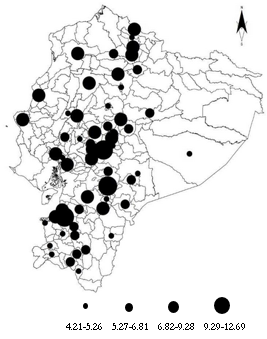
Source: Own elaboration based on INEC data
3 Data and variables
To determine if agglomeration economies affect productivity, we used data from the 1980 and 2010 Economic Census of the National Institute of Statistics and Censuses (INEC), at the level of each sector and canton or municipality, except for those corresponding to the Galapagos Islands. The empirical work included the homogenization of the databases prepared from the referred censuses because these were not directly comparable. In total, 26 sectors and 114 cantons are integrated. The sectoral breakdown corresponds to two digits and three digits - ISIC for 1980 and 2010, respectively.
| Variable | Mean | Standard Deviation |
| productivity growth | .127 | 1.391 |
| specialization | -.097 | .815 |
| diversity | -.983 | .470 |
| density | -1.711 | 1.958 |
| average size firms | -.2509 | .609 |
The dependent variable is measured as follows:
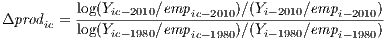 | (1) |
where, Y ic and empic are the levels of production and employment by industry and canton, respectively, between 1980 and 2010.
3.1 Measuring agglomeration economies
The measure of agglomeration economies is the index of specialization related to location economies:
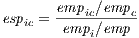 | (2) |
where, empic is the employment of industry i in canton c, and emp is total employment.
While the economies of urbanization are commonly measured through the inverse of the Herfindahl index, constructed from the participation of industries in local employment, with the exception of the industry that is considered, this variable is normalized by the same variable at the country level:
![∑i 2
1∕--i*=1,i*⁄=i[empi*c∕(empc---empic)]-
divic = 1∕∑i [emp ∕(emp - emp )]2
i*=1,i*⁄=i i* i](2428x.png) | (3) |
where i is the number of industries. The numerator is maximum when all sectors, except the subject of the analysis, i*, are the same size in the cities. This indicator reflects the sectorial diversity of the industry and the city. Therefore, it is not necessarily related to the level of specialization of the industry being analyzed.
With the intuition that large companies are usually better able than small companies to internalize some of the local effects, Glaeser et al. (1992) suggest incorporating the average size of firms within the local industry as an additional determinant of location economies. When normalized by the average of the companies in the industry at the level of the whole country, we obtain:
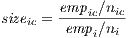 | (4) |
where nic is the number of companies in the industry and in city c. However, according to Combes, Gobillon (2015), its use leads to serious problems of endogeneity, since it depends on the location options of the companies and their scale of production, which directly influence local productivity. Thus, one should avoid introducing it into the specification unless you have a strong instrumentation strategy.
Finally, as in Combes (2000), to simultaneously control for differences between cities, it is relevant to consider the density of total employment by means of the following indicator:
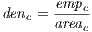 | (5) |
where areac is the area of the city measured in km2.
3.2 Selection bias
A particularity of the data used in this study is that they are not fully observable, since some industrial sectors are present only in certain cities. This is a typical problem in research that uses data on a local scale. We isolate the selection bias through a model Heckman (1979) proposes, applied in two stages as in Viladecans-Marsal (2004), Combes (2000), Henderson et al. (1995), and others. In the first stage, a model is formulated to estimate the probability that a city contains an industrial sector:
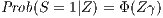 | (6) |
where S indicates the sector (S = 1 if the sector is in the city and S = 0 otherwise), Z is a vector of explanatory variables, γ is a vector of unknown parameters, and Φ is the cumulative distribution function of the normal distribution. The estimation of the model yields results that can be used to predict the probability that an industry is contained in a specific city. In the second stage, the initial model is estimated by OLS with the dependent variable of continuous productivity growth, which corrects the selection bias by incorporating the variable called the Mills inverse ratio (λ), which is derived from the previous stage.
3.3 Endogeneity and instrumental variables
When estimating the impact of agglomeration economies on local results such as productivity growth, the literature recognizes two potential sources of endogeneity: omitted variables and inverse causality. Either may arise at the local and individual level (Combes, Gobillon 2015), and their treatment focuses on instrumental variables, including historical and geographical variables, for each endogenous regressor, specialization, diversity, and density.
According to Combes, Gobillon (2015), historical values of population or density are relevant, because by remaining in time, they create inertia in the population and in local economic activity. This idea is imputed to the construction of the instruments for the variables of specialization and diversity. For that reason, the instruments are generated from the data of the birth of firms. The birth of firms is considered correlated with the level of specialization and diversity of the industries in the cities, but not directly with the growth of employment and productivity. The dummy of geological character is related to all the endogenous variables and does not represent a direct effect on the variables of interest or the geographical variables related to the availability of roads in 1980, also generated as dummies.
Estimating the effect of location, urbanization economies, and density on productivity using instrumental variables can lead to unbiased estimates, provided that the instruments meet the conditions of relevance (7) and exogeneity (8). Formally, these conditions are:
Z denotes the set of instruments.
Equation (7) denotes that the relevance of an instrument depends on the partial correlation of the instrumental variables and the endogenous regressors. These are obtained by Ordinary Least Squares (OLS) estimates for each endogenous regressor of the growth of productivity in instrumental variables, including regional, provincial, and industrial fixed effects. The results show that the relevant instruments for specialization are the specialization index, the population density of 1950, the urbanization index of 1980, the availability of roads in 1980, and a geological dummy. For the diversity and density of employment these same instruments are relevant, except the specialization index.
The analysis of the relevance of the defined instruments is validated by the test developed by Stock, Yogo (2005)2 , who define two tests for weak instruments based on a single F statistic. The values in all cases are greater than 103 , suggesting that the instruments are strong; their strength is confirmed when they contradict the critical values reported by Stock, Yogo (2005).
The condition of exogeneity suggested in equation (8), that is, the orthogonality with respect to the error term, is evaluated with the Sargan over-identification test, which allows us to reject the hypothesis of restriction of over-identification, suggesting the joint exogeneity of the instruments.
4 Estimation and analysis
The model specified to estimate the effect of agglomeration economies on the productivity growth of a particular industry in a certain canton between 1980 and 2010 appears below. In particular, the Two-Stage Least Squares (2SLS) estimator is used due to the aforementioned aspects of endogeneity, focused on regressions with instrumental variables.
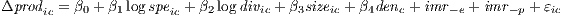 | (9) |
where Δprodic represents the growth of productivity in industry i and city c between both years, respectively; speic, divic, sizeic are the indices of specialization, diversity, and average industry size i in city c; and denc is the density of total employment. The variables imr-e and imr-p are the inverse ratio of Mills for employment and productivity in each case, introduced to control the selection bias, and εic is assumed as the error term. To control for unobservable heterogeneity, we introduce fixed effects at the province, industry, and regional4 levels. The literacy rate of each city aims to capture the qualifications of the population in each case5 .
| Productivity | OLS | TOBIT | 2SLS |
| specialization | -0.075* | 0.091 | -0.285 |
| (0.026) | (0.073) | (0.166) | |
| diversity | 0.064 | -0.189 | 0.397* |
| (0.046) | (0.178) | (0.183) | |
| density | 0.031 | -0.019 | -0.161* |
| (0.019) | (0.043) | (0.081) | |
| size firms | -0.021 | 0.229* | 0.049 |
| (0.036) | (0.101) | (0.077) | |
| inverse Mills ratio | -0.032 | -0.767 | |
| (0.119) | (0.341) | ||
| N | 2963 | 2963 | 2963 |
| F | — | — | 14.75 |
| CONTROL | |||
| Literacy index 1980 | Yes | — | Yes |
| FIXED EFFECTS | |||
| Region | Yes | No | Yes |
| Province | Yes | No | Yes |
| Industry | Yes | Yes | Yes |
| Over identificaction (Sargan Test) | — | — | 1.145 |
| P value - SarganTest | — | — | (0.5640) |
The explanatory variables correspond to the initial year, 1980, and have been normalized by the corresponding values at the national level. All the variables are expressed in logarithms, which is why the estimated parameters are their elasticities with respect to each variable. This makes them easily comparable and interpretable.
The first estimates of equation (9) are made by OLS. However, given the presence of selection bias and the endogeneity of the model, such results are not entirely correct, as it is pertinent to apply two additional estimation strategies. To correct the selection bias, we proceeded with maximum likelihood estimations through a Tobit Type II model, while the endogeneity of the model implies estimations with instrumental variables (2SLS) with results accepted as definitive (Table 2).
As a robustness test, a strategy for estimating productivity growth is applied that is less sensitive to weak instruments: the limited information maximum likelihood (LIML) estimator. This strategy takes into account only the likelihood function of the endogenous variables of equation (9) and the identification of restrictions corresponding to the equation to be estimated.
The results obtained are supported with those obtained by 2SLS and are consistent with previous empirical findings given that the productivity gains of urban agglomeration economies are generally found to be positive (Melo et al. 2009), The results obtained differ in that the location economies are not significant. At this point, it should be noted that 94% of the firms of the two years analyzed correspond to the category of microenterprise, 4% correspond to small firms, and the 2% remaining percentage are medium and large firms6 . This corresponds to the finding of Jacobs (1969) that small businesses benefit more from urban diversity in large cities due to their greater dependence on external industrial environments for multiple intermediate inputs, while large companies are self-sufficient.
5 Conclusion
In particular, two different contributions to the literature are presented. The first relates to the agglomeration literature about Latin American countries like Ecuador that have received little attention from this approach.
The growth of productivity is determined significantly and positively by urbanization economies, while the density elasticity is negative. This is interpreted as the result of the effects of congestion. These results are consistent with other works for developed countries Cingano, Schivardi (2004) and Guevara et al. (2015) for Ecuador. They approximate labor productivity in 2010, both in industry and in services, as a function of specialization, diversity, competence, and density (of firms or employment) in the cities of Ecuador. Using as main instruments the spatial delays of each of the endogenous variables, their results suggest a strong positive externality of the diversity in the productivity of the manufacturing industries (1,651) and of the services (2,081). In manufacturing, the density of employment is also statistically significant.
Productivity takes place in provincial capitals, characterized by the concentration of public sector intervention, both in terms of investments (public goods) and public consumption (services); ease of access to large markets; and the possibility of finding large niches of specialization, and access to a broad labor market and specialized urban functions.
Second, in terms of Ecuador’s public policy, a boost to industry and services is expected within the framework of the country’s industrial policy. For the period 2016-2025, this policy aims to generate 251,000 new jobs; to invest 13,600 million dollars; contribute positively to the trade balance of 1,200 million dollars; and increase GDP by 10 percentage points. Ecuador’s public policy recognizes the imminent change in the spatial distribution of economic activities and that it is necessary to focus on land use and labor mobility relating to trade in intermediate goods. Consequently, the industrial policy must mesh with others that consider the spatial dimension. In the area of externalities in particular, the challenge is to balance negative externalities and exploit the positive externalities of agglomeration based on greater knowledge, an important mechanism through which the agglomeration economies act.
References
Arrow K (1962) The economic implications of learning by doing. Review of Economics and Statistics 29: 155–173
Cameron AC, Trivedi PK (2010) Microeconometrics Using Stata (Revised ed.). Stata Press, College Station, TX
Cingano F, Schivardi F (2004) Identifying the sources of local productivity growth. Journal of the European Economic Association 2[4]: 720–744. CrossRef.
Combes P, Gobillon L (2015) The empirics of agglomeration economies. In: Duranton G, Henderson V, Strange W (eds), Handbook of Regional and Urban Economics, Volume 5. North Holland, Amsterdam, 247–348
Combes PP (2000) Economic structure and local growth: France, 1984-1993. Journal of urban economics 47[3]: 329–355
Glaeser E, Kallal H, Scheinkman J, Shleifer A (1992) Growth in cities. Journal of Political Economy 100[6]: 1126–1152. CrossRef.
Guevara C, Riou S, Autant-Bernard C (2015) Agglomeration externalities and urbanization in Ecuador. 55th congress of the European Regional Science Association, Lisbon, Portugal, https://halshs.archives-ouvertes.fr/halshs-01212174
Heckman J (1979) Sample selection bias as a specification error. Econometrica 47[1]: 153–161
Henderson J, Kuncoro A, Turner M (1995) Industrial development in cities. Journal of Political Economy 103[5]: 1067–1090. CrossRef.
Jacobs J (1969) The Economy of Cities. Random House, New York
Marshall A (1890) Principles of Economic. MacMillan, London
Melo PC, Graham DJ, Noland RB (2009) A meta-analysis of estimates of urban agglomeration economies. Regional Science and Urban Economics 39[3]: 332–342. CrossRef.
Romer P (1986) Increasing returns and long-run growth. Journal of Political Economy 94: 1002–1037
Staiger D, Stock J (1997) Instrumental variables regression with weak instruments. Econometrica 65: 557–586
Stock J, Yogo M (2005) Testing for weak instruments in linear iv regression. In: Andrews D, Stock J (eds), Identification and Inference in Econometric Models: Essays in Honor of Thomas J. Rothenberg. Cambridge University Press, Cambridge, UK, Chapter 5
Viladecans-Marsal E (2004) Agglomeration economies and industrial location: City-level evidence. Journal of Economic Geography 4[5]: 565–582. CrossRef.
 © 2019 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)
© 2019 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)